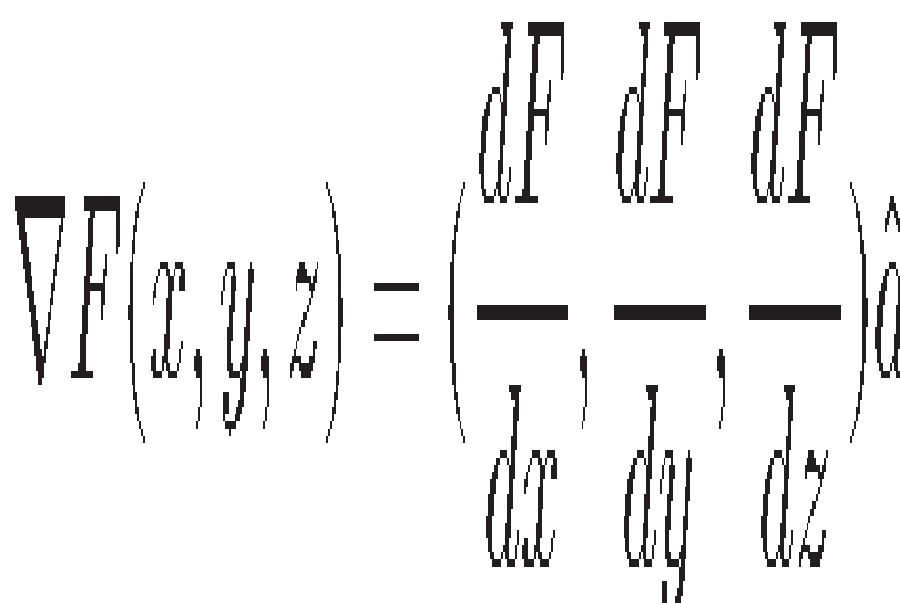
Gradient (độ dốc) là khái niệm rất gần với khái niệm đạo hàm mà chúng ta đã học thời cấp 3, nó biểu diễn cho tốc độ thay đổi của hàm. Gradient là một vectơ trong khi đạo hàm là giá trị vô hướng (hiểu nôm na là các giá trị số). Véc tơ này chỉ ra hướng mà tại đó giá trị của hàm thay đổi nhiều nhất và trở thành véc tơ 0 khi hàm đạt giá trị cực đại hoặc cực tiểu địa phương.
Một cách diễn đạt trực quan, tưởng tượng như ta đang ở trên một quả núi. Tại chân núi, những chỗ trũng của thung lũng và tại đỉnh núi, độ dốc bằng không. Tùy vào hình dạng của quả núi và vị trí ta quan sát, độ dốc sẽ có những giá trị khác nhau. Khi đang ở đỉnh núi thì đi về hướng nào cũng là “ đường xuống núi ” cả .

 Độ dốc của một đỉnh núi
Độ dốc của một đỉnh núi
Quay trở lại khái niệm đạo hàm mà ta học thời cấp 3. Đại lượng này cho chúng ta tốc độ thay đổi của hàm dựa trên một biến số duy nhất, thường được đặt là x. Ví dụ, dF/dx cho chúng ta biết hàm F thay đổi bao nhiêu khi x thay đổi 1 đơn vị. Đối với một hàm có nhiều biến, chẳng hạn như x và y, nó sẽ có nhiều đạo hàm: các giá trị dF/dx và dF/dy cho ta biết giá trị của hàm sẽ thay đổi thế nào nếu ta thay đổi một biến số (với giả định các biến số khác không thay đổi).
Bạn đang đọc: Gradient trong Deep Learning là gì? – Trí tuệ nhân tạo
Chúng ta hoàn toàn có thể trình diễn những tỷ suất này trong một vectơ nhiều thành phần, với một thành phần là một đạo hàm. Do đó, một hàm có 3 biến sẽ có một gradient với 3 thành phần :
- F (x) có một biến và một đạo hàm duy nhất: dF / dx
- F (x, y, z) có ba biến và ba đạo hàm: (dF / dx, dF / dy, dF / dz)
Giống như đạo hàm thường thì, gradient chỉ ra hướng biến hóa mạnh nhất của hàm. Do đó nó hoàn toàn có thể được sử dụng thể tìm ra những cực lớn và cực tiểu địa phương. Trong một hàm đơn biến, để đổi khác giá trị của hàm, tất cả chúng ta chỉ có hai hướng “ tiến ” và “ lùi ” dựa trên sự biến hóa trên trục x. Đối với hàm đa biến, mọi việc không đơn thuần như vậy. Với hàm hai biến, tất cả chúng ta hoàn toàn có thể tưởng tượng đó là vô số những hướng trong một mặt phẳng, với hàm ba biến, đó hoàn toàn có thể là bất kể hướng nào trong khoảng trống 3 chiều. Với hàm 100 biến ( như nguồn vào của mạng nơ ron sử dụng word embedding 100 chiều ), nó vượt ra khỏi sức tưởng tượng của tất cả chúng ta. Mặc dù vậy, gradient là công cụ toán học tuyệt vời để ta hoàn toàn có thể khảo sát sự biến thiên của những hàm này .
Gradient được ký hiệu bằng chữ delta ( Δ ) ngược và được gọi là “ del ”. Với ví dụ trên, ta có :
Thành phần của gradient là đạo hàm riêng so với x, y và z. Đối với một hàm một biến gradient chính là đạo hàm của hàm này .
Ứng dụng thông dụng của gradient là tìm kiếm những giá trị cực lớn và cực tiểu của hàm. Đây là trách nhiệm quan trọng để tối ưu những trọng số trong mạng Deep learning .
Hi vọng trải qua bài viết này những bạn đã hiểu hơn về Gradient. Đây là khái niệm quan trọng nếu như bạn muốn hiểu những thâm thúy những góc nhìn kỹ thuật của Deep learning, từ đó hoàn toàn có thể phong cách thiết kế được những quy mô tốt hơn .Hãy theo dõi trituenhantao.io để nhận được thông báo ngay khi có bài viết mới nhé!
—–
” Gradient trong Deep Learning là gì ?, ” Trí tuệ tự tạo, Ngày xuất bản : 23/07/2019, URL : https://final-blade.com/kien-thuc/gradient-trong-deep-learning/, Ngày truy vấn : 28/01/2023 .
Bạn muốn trích dẫn bài này : —–Bài viết có liên quan
Issue: *
Your Name:
*
Your Email: *
Details: *


Source: https://final-blade.com
Category : Kiến thức Internet
