5/5 – (14 bình chọn)
Chào mừng các em đã trở lại lớp học Toán của itoan. Đây là bài học đầu tiên trong chương trình Toán lớp 6, các em có đang gặp khó khăn gì với bài giảng trên lớp không? Đừng vội lo lắng quá! Hôm nay chúng ta cũng học bài Phần tử của tập hợp. Bài học này là nền tảng cho các kiến thức trong chương trình Toán cấp 2 nên các bạn cố gắng theo dõi nha! Không chần chừ gì nữa, hãy cùng cô bước vào bài học hôm nay ngay thôi.
Mục tiêu của bài học Phần tử của tập hợp
Các bạn nhỏ thân yêu hãy cùng cô bước vào phần đầu tiên của bài học hôm nay ngay nhé, đó là phần mục tiêu bài học!
- Nắm vững định nghĩa, kí hiệu, đặc điểm của tập hợp, phần tử tập hợp.
- Vận dụng linh hoạt để giải các bài toán, áp dụng vào thực tế.
Lý thuyết cần nhớ Phần tử của tập hợp
Dưới đây là phần kiến thức của bài giảng, các em nhớ ghi chép lại và học bài thật kỹ trước khi làm bài tập nhé!
1. Ví dụ
Tập hợp là khái niệm cơ bản thường dùng trong toán học và cuộc sống.
Ta thường xuyên gặp tập hợp, ví dụ như:
- Tập hợp các bộ quần áo trong tủ quần áo
- Tập hợp các học sinh trong lớp 6C.
- Tập hợp các số tự nhiên từ 5 đến 30.
- Tập hợp các chữ cái a, b, c, d.

2. Cách viết các ký hiệu
- Người ta thường dùng các chữ cái in hoa như:
A
,
B
,
C
,G,E
… để biểu thị cho tên tập hợp.
- Có 2 cách viết thường được dùng để viết tập hợp:
Dùng phương pháp liệt kê các phần tử của 1 tập hợp
Ví dụ: Tập hợp A các số tự nhiên lớn hơn 2 và nhỏ hơn 8:
A = {3;4;5;6;7} hoặc A= {7;3;4;5;6}
Viết tập hợp dựa trên tính chất đặc trưng của các phần tử
Ví dụ: Tập hợp A các số tự nhiên lớn hơn 2 và nhỏ hơn 8:
A ={ x ∈ N /2<x<8}
- Trong ví dụ trên, các số 3,4,5,6,7 thuộc vào tập hợp A. Các số đó là các phần tử của A.
- Kí hiệu: 3
∈
A
;4
∈
A
;5
∈
A
;6
∈
A;7
∈
A. Số 1 không thuộc tập hợp
A
, kí hiệu: 1
∉
A
3. Chú ý
-
Các phần tử trong một tập hợp được viết nằm giữa hai dấu ngoặc nhọn { }. Chúng được ngăn cách với nhau bằng dấu “;” (nếu là phần tử số) hoặc dấu “,” nếu không phải phần tử số.
- Mỗi phần tử trong tập hợp được liệt kê 1 lần, không cần thiết phải sắp xếp theo thứ tự.
- Ngoài ra ta có thể minh họa tập hợp bằng một vòng tròn kín. Trong tập hợp, mỗi phần tử được biểu diễn bằng 1 dấu chấm bên trong vòng tròn kín đó, gọi là sơ đồ Venn.
Ví dụ: Tập hợp A = {0;1;2;3} có thể biểu diễn như sau:
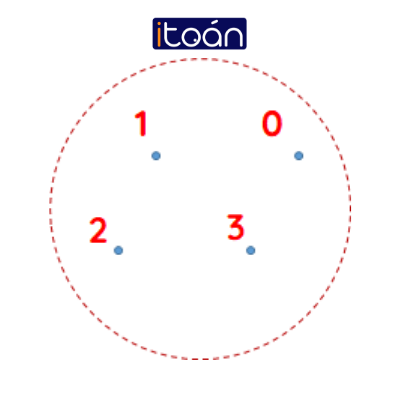
Nếu các em tự tìm hiểu lý thuyết xong vẫn khiến các em bị hoang mang thì chớ bỏ cuộc nhé, các bạn hãy xem hướng dẫn bài giảng của cô giáo Phạm Giang Yên Bình đến từ Toppy qua đoạn video dưới đây nhé!
Giải bài tập SGK
Phần tử của tập hợp
Sau khi đã nắm rõ lý thuyết rồi thì chúng ta cùng đến với bài tập trong sách giáo khoa ngay thôi nào!
Bài tập 1 (SGK Toán 6 trang 6 Tập 1):
Viết tập hợp A các số tự nhiên lớn hơn 8 và nhỏ hơn 14 bằng hai cách sau đó điền kí hiệu thích hợp vào ô vuông:

Hướng dẫn giải:
– Tập hợp A gồm: 9; 10; 11; 12; 13.
A = {9; 10; 11; 12; 13}.
– Xét số 12,ta nhận định 12 là 1 phần tử trong tập hợp A;
Xét số 16, ta nhận định 16 không phải phần tử trong tập hợp A.
Vậy nên ta có thể viết:

Bài 2 (SGK Toán 6 trang 6 Tập 1):
Viết tập hợp các chữ cái trong từ “TOÁN HỌC”.
Hướng dẫn giải:
Phân tích từ “TOÁN HỌC” ta được các chữ cái: T, O, A, N, H, O, C.
Chữ “O” xuất hiện 2 lần, nhưng theo nguyên tắc thì mỗi phần tử chỉ được liệt kê 1 lần nên ta chỉ viết 1 lần.
Gọi E là tập hợp chữ cái trên, ta có:
E = {T, O, A, N, H, C}
Bài 3 (SGK Toán 6 trang 6 Tập 1):
Cho hai tập hợp A = {a, b}; B = {b, x, y}. Điền kí hiệu thích hợp vào ô vuông:

Hướng dẫn giải:
Quan sát hai tập hợp, ta có kết quả:

Bài 4 (SGK Toán 6 trang 6 Tập 1):
Nhìn vào các hình 3, 4 và 5, viết các tập hợp A, B, M, H.

Hướng dẫn giải:

Chú ý: ‘’bút ‘’ là phần tử của M , cũng là phần tử của H
Bài 5 (SGK Toán 6 trang 6 Tập 1):
a) Một năm gồm 4 quý. Viết tập hợp A các tháng của quý hai trong năm.
b) Viết tập hợp B các tháng (dương lịch) có 30 ngày.
Hướng dẫn giải:


Luyện tập
Phần tử của tập hợp
Bài tập sách giáo khoa rất sát với kiến thức trên lớp học. Nếu bạn nào đã hoàn thành rồi thì có thể làm thêm phần luyện tập để nắm vững kiến thức và cọ xát với một số dạng bài nâng cao hơn nhé!
Bài tập 1: Cho M là tập hợp các số tự nhiên chia hết cho 5, không vượt quá 20. Khẳng định nào sai?
A. M={0;5;10;15;20}
B. Tập hợp M có tất cả 5 phần tử
C. 20∈M
D. 0∉M
Bài tập 2: Tập hợp các chữ cái của từ “DO AND DIFFERENT” có số phần tử là:
A. 10
B. 14
C. 9
D. 13
Bài tập 3: Tập hợp A bao gồm các chữ cái trong từ “CON HOC GIOI”. Tập hợp B bao gồm các chữ số trong cụm từ “TOAN LOP 6”. Gọi D là tập hợp bao gồm tất cả các phần tử của A và phần tử của B. Số phần tử của D là:
A. 7
B. 18
C. 13
D. 11
Bài tập 4: Số phần tử của tập hợp N={1;5;9;…;65} là:
A. 65
B. 17
C. 64
D. 18
Hướng dẫn giải bài tập tự luyện
Bài tập 1
Đáp án: D
Bài tập 2
Đáp án: C
Bài tập 3
Đáp án: A
Bài tập 4
Đáp án: B
Lời kết:
Vậy là đã đến lúc cô phải chia tay với các em, bài học Phần tử của tập hợp cũng đã kết thúc rồi. Cô tin là có lẽ các bạn học hết bài học hôm nay cũng đọng lại cho mình nhiều phần kiến thức quan trọng rồi đúng không nào? Cô rất tự hào về các em! Nếu bạn nào muốn tìm hiểu thêm kiến thức và bài tập nâng cao khác có thể đến trang web Toppy để được hướng dẫn làm bài nhiều hơn nhé! Tạm biệt các em.
>> Xem thêm: Số phần tử của tập hợp, tập hợp con