Rate this post
Khi nhắc đến những thuật toán được sử dụng phổ biến trong lập trình thì không thể nào thiếu Quick Sort. Cũng giống như các thuật toán khác, Quick Sort không hề dễ “xơi” mà cần có thời gian nghiên cứu kỹ lưỡng để hoàn toàn nắm chắc nó trong bàn tay. Trong bài viết sau, Teky sẽ giúp bạn giải đáp một số khái niệm cơ bản xung quanh thuật toán Quick Sort. Đây là sẽ những kiến thức hữu ích mà bất kỳ lập trình viên nào cũng cần hiểu rõ.
Tóm Tắt
Tìm hiểu thuật toán Quick Sort là gì ?
Giới thiệu về thuật toán sắp xếp
Vì Quick Sort cũng là một dạng thuật toán sắp xếp nên tiên phong tất cả chúng ta sẽ điểm nhanh qua các phân loại thông dụng .
- Thuật toán đơn giản với độ phức tạp O(n^2) bao gồm: Insertion Sort (sắp xếp chèn), Bubble Sort (sắp xếp nổi bọt), Selection Sort (sắp xếp lựa chọn).
- Thuật toán hiệu quả với độ phức tạp O(nlogn) bao gồm: Heap Sort (sắp xếp vun đống), Merge Sort (sắp xếp trộn), Quick Sort (sắp xếp nhanh).
- Thuật toán đặc biệt với độ phức tạp O(n) bao gồm: Counting Sort (sắp xếp đếm), Bucket Sort (sắp xếp phân cụm), Radix Sort (sắp xếp cơ số).
- Xử lý các tập dữ liệu lớn bao gồm: External sort (sắp xếp ngoài).
 Thuật toán sắp xếp trong dùng để giải quyết và xử lý các tệp tài liệu nhỏ. Họ tài liệu sẽ được đưa hàng loạt vào trong bộ nhớ của máy tính. Còn thuật toán sắp xếp ngoài chỉ sử dụng được cho các tệp tài liệu lớn. Họ tài liệu không hề đưa hàng loạt tài liệu vào bộ nhớ trong cùng một lúc nhưng hoàn toàn có thể đọc lần lượt từng bộ phận tại bộ nhớ ngoài .
Thuật toán sắp xếp trong dùng để giải quyết và xử lý các tệp tài liệu nhỏ. Họ tài liệu sẽ được đưa hàng loạt vào trong bộ nhớ của máy tính. Còn thuật toán sắp xếp ngoài chỉ sử dụng được cho các tệp tài liệu lớn. Họ tài liệu không hề đưa hàng loạt tài liệu vào bộ nhớ trong cùng một lúc nhưng hoàn toàn có thể đọc lần lượt từng bộ phận tại bộ nhớ ngoài .
Khái niệm thuật toán Quick Sort
Quick Sort có khái niệm khá tương đương với Merge Sort. Tức là đều hoạt động giải trí dựa trên chính sách chia và trị. Nó sẽ chịu nghĩa vụ và trách nhiệm phân loại tài liệu thành các mảng nhỏ và sắp xếp một cách nhanh gọn. Đó cũng là nguyên do tại sao Quick Sort mang ý nghĩa là sắp xếp nhanh .Quick Sort được chia vào phân loại giải thuật sắp xếp với phức tạp thời hạn là trung bình O ( n log n ) và xấu nhất O ( n2 ). Độ phức tạp tài liệu của thuật toán QuickSort tùy thuộc vào cách hiện thực. Tần suất tối ưu là đôi lúc .Thuật sắp xếp nhanh Quick Sort sẽ triển khai chia nhỏ mảng thành hai phần. Thông qua giải pháp so sánh từng thành phần với một thành phần chốt, ta sẽ thu được một mảng gồm những thành phần nhỏ hơn hoặc bằng thành phần chốt và một mảng gồm những thành phần lớn hơn thành phần chốt. Mỗi phiên bản Quick Sort C + + khác nhau sẽ có một cách chọn thành phần chốt khác nhau. Có thể là thành phần tiên phong, sau cuối hoặc thành phần ngẫu nhiên, thành phần trung vị .Hoạt động phân loại này diễn ra liên tục và chỉ dừng lại khi độ dài của mỗi thành phần con bằng 1. Để sắp xếp nhanh các thành phần con thu được thành một mảng hoàn hảo, người dùng sẽ sử dụng chiêu thức đệ quy. Tất cả các thao tác này đều diễn ra trong thời hạn tuyến tính .
Ý tưởng của thuật toán Quick Sort
Cách tiến hành thuật toán Quick Sort Java
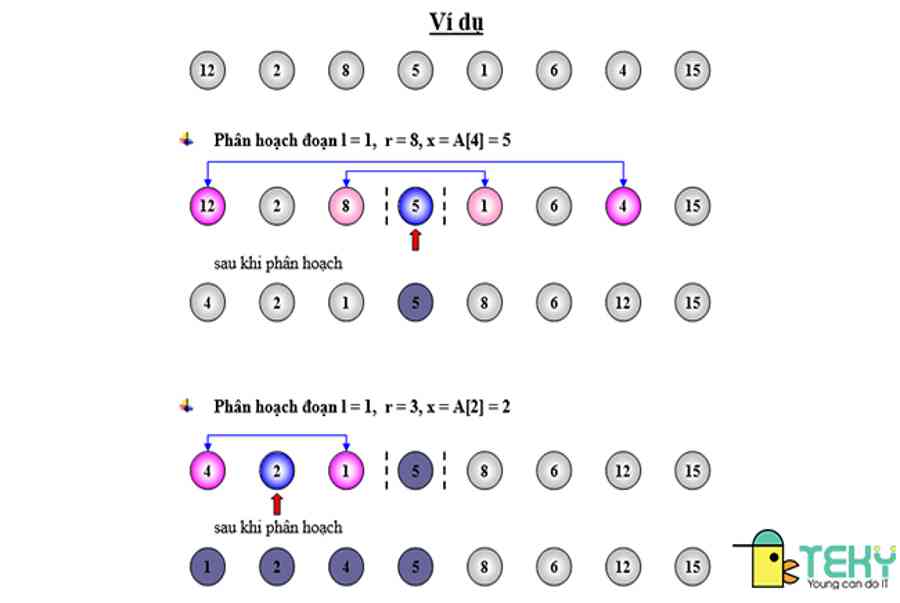
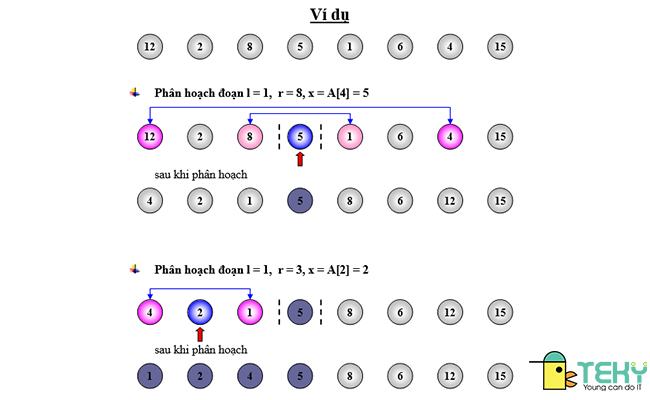
Đầu tiên, ta sẽ triển khai chọn một pivot. Về cách chọn pivot, có rất nhiều cách để dùng trong nhiều trường hợp khác nhau. Tuy nhiên thông dụng nhất là chọn pivot đầu, pivot cuối và pivot giữa .Sau khi đã chọn được thành phần người dùng sẽ cần khai báo 2 biến của 2 con trỏ để duyệt 2 phía của thành phần pivot. Lần lượt, ta sẽ trỏ biến bên trái đến mỗi thành phần nằm bên trái của thành phần pivot. Ngược lại, ta cũng sẽ trỏ biến bên phải đến mỗi thành phần nằm bên phải của thành phần pivot . Với mỗi lần trỏ như vậy, ta triển khai phân loại các thành phần. Tại bên trái, nếu biến trỏ nhỏ hơn thành phần thì chuyển giá trị sang phải. Còn tại bên phải, nếu biến trỏ nhỏ hơn thành phần thì chuyển giá trị sang trái. Nếu biến trỏ bằng thành phần thì tráo đổi giá trị 2 bên phải và trái. Cuối cùng, khi tổng thể thành phần trái lớn hơn thành phần phải thì đây chính là giá trị chốt mới .Lý thuyết cơ bản là như vậy nhưng với mỗi cách chọn thành phần, quy trình tiến hành sẽ khác nhau. Dưới đây là ví dụ về 3 cách chọn thành phần thông dụng nhất .
Với mỗi lần trỏ như vậy, ta triển khai phân loại các thành phần. Tại bên trái, nếu biến trỏ nhỏ hơn thành phần thì chuyển giá trị sang phải. Còn tại bên phải, nếu biến trỏ nhỏ hơn thành phần thì chuyển giá trị sang trái. Nếu biến trỏ bằng thành phần thì tráo đổi giá trị 2 bên phải và trái. Cuối cùng, khi tổng thể thành phần trái lớn hơn thành phần phải thì đây chính là giá trị chốt mới .Lý thuyết cơ bản là như vậy nhưng với mỗi cách chọn thành phần, quy trình tiến hành sẽ khác nhau. Dưới đây là ví dụ về 3 cách chọn thành phần thông dụng nhất .
>>>Mời bạn đọc tham khảo thêm:
Cách 1 : Chọn thành phần đầu trong thuật toán Quick Sort
quickSort = ( unSortedArr ) => {/ / nếu mảng không quá 1 thành phần thì mảng đó đã được sản xuấtif ( unSortedArr. length < 2 ) return unSortedArr ;const pivot = unSortedArr [ 0 ] ; / / lấy thành phần đầu của mảng làm thành phần chốtconst leftArr = [ ] ; / / mảng chứa thành phần nhỏ hơn pivotconst rightArr = [ ] ; / / mảng chứa thành phần lớn hơn pivotlet currentItem ; / / thành phần đang được xét/ / loop các thành phần còn lại trong mảng trừ thành phần chốt ./ / Do pivot là ptu tiên phong nên i sẽ khởi đầu từ 1for ( let i = 1 ; i < unSortedArr. length ; i + + ) {currentItem = unSortedArr [ i ] ;if ( currentItem < pivot ) {leftArr. push ( currentItem ) ;} else {rightArr. push ( currentItem ) ;}}return [ … this. quickSort ( leftArr ), pivot, … this. quickSort ( rightArr ) ] ;}
Cách 2 : Chọn thành phần cuối
quickSort = ( unSortedArr ) => {if ( unSortedArr. length < 2 ) return unSortedArr ;const pivot = unSortedArr [ unSortedArr. length – 1 ] ; / / thành phần cuối mảng làm chốtconst leftArr = [ ] ;const rightArr = [ ] ;let currentItem ;/ / Do pivot là ptu cuối nên length sẽ trừ đi 1for ( let i = 0 ; i < unSortedArr. length – 1 ; i + + ) {currentItem = unSortedArr [ i ] ;if ( currentItem < pivot ) {leftArr. push ( currentItem ) ;} else {rightArr. push ( currentItem ) ;}}return [ … this. quickSort ( leftArr ), pivot, … this. quickSort ( rightArr ) ] ;}
Cách 3 : Chọn thành phần giữa trong thuật toán Quick Sort
quickSort = ( unSortedArr ) => {if ( unSortedArr. length < 2 ) return unSortedArr ;/ / lấy thành phần giữa làm chốtconst pivotIndex = Math. floor ( unSortedArr. length / 2 ) ;const pivot = unSortedArr [ pivotIndex ] ;const leftArr = [ ] ;
const rightArr = [];
let currentItem ;unSortedArr. splice ( pivotIndex, 1 ) ; / / vô hiệu ptu pivot trong mảngfor ( let i = 0 ; i < unSortedArr. length ; i + + ) {currentItem = unSortedArr [ i ] ;if ( currentItem < pivot ) {leftArr. push ( currentItem ) ;} else {rightArr. push ( currentItem ) ;}}return [ … this. quickSort ( leftArr ), pivot, … this. quickSort ( rightArr ) ] ;}
Giải thuật toán Quick Sort
 Dưới đây là một ví dụ về quy trình giải thuật toán Quicksort C + + được viết bằng ngôn từ lập trình Java :public class QuickSort {public static void main ( String [ ] args ) {int [ ] x = { 6, 2, 3, 4, 5, 9, 1 } ;printArray ( x ) ;int left = 0 ;int right = x.length – 1 ;quickSort ( x, left, right ) ;printArray ( x ) ;}public static void quickSort ( int [ ] arr, int left, int right ) {if ( arr = = null | | arr.length = = 0 )return ;if ( left > = right )return ;int middle = left + ( right – left ) / 2 ;int pivot = arr [ middle ] ;int i = left, j = right ;while ( i < = j ) {while ( arr [ i ] < pivot ) {i + + ;}while ( arr [ j ] > pivot ) {j – ;}if ( i < = j ) {int temp = arr [ i ] ;arr [ i ] = arr [ j ] ;arr [ j ] = temp ;i + + ;j – ;}}if ( left < j )quickSort ( arr, left, j ) ;if ( right > i )quickSort ( arr, i, right ) ;}public static void printArray ( int [ ] arr ) {for ( int i = 0 ; i < arr.length ; i + + ) {System. out.print ( arr [ i ] + ” “ ) ;}System. out.println ( ) ;}}
Dưới đây là một ví dụ về quy trình giải thuật toán Quicksort C + + được viết bằng ngôn từ lập trình Java :public class QuickSort {public static void main ( String [ ] args ) {int [ ] x = { 6, 2, 3, 4, 5, 9, 1 } ;printArray ( x ) ;int left = 0 ;int right = x.length – 1 ;quickSort ( x, left, right ) ;printArray ( x ) ;}public static void quickSort ( int [ ] arr, int left, int right ) {if ( arr = = null | | arr.length = = 0 )return ;if ( left > = right )return ;int middle = left + ( right – left ) / 2 ;int pivot = arr [ middle ] ;int i = left, j = right ;while ( i < = j ) {while ( arr [ i ] < pivot ) {i + + ;}while ( arr [ j ] > pivot ) {j – ;}if ( i < = j ) {int temp = arr [ i ] ;arr [ i ] = arr [ j ] ;arr [ j ] = temp ;i + + ;j – ;}}if ( left < j )quickSort ( arr, left, j ) ;if ( right > i )quickSort ( arr, i, right ) ;}public static void printArray ( int [ ] arr ) {for ( int i = 0 ; i < arr.length ; i + + ) {System. out.print ( arr [ i ] + ” “ ) ;}System. out.println ( ) ;}}
Độ phức tạp của thuật toán sắp xếp nhanh
Công thức tính thời hạn của thuật toán Quick Sort được viết như sau :T ( n ) = T ( k ) + T ( n-k-1 ) + θ ( n )Trong đó, T ( k ) và T ( n-k-1 ) thời hạn dành cho hai cuộc gọi đệ quy. Còn θ ( n ) là tiến trình phân vùng. k là số thành phần nhỏ hơn thành phần chốt. Thời gian của thuật toán Quick Sort còn phụ thuộc vào vào mảng đầu và kế hoạch chia mảng .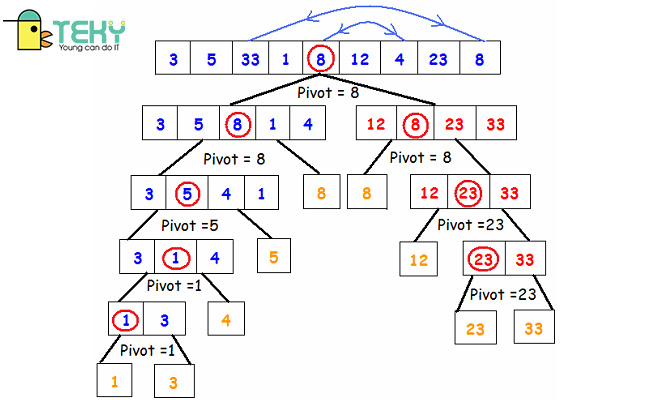
- Với phân đoạn không cân bằng: Khi trường hợp xấu nhất xảy ra (pivot là phần tử đầu và dãy đã được sắp xếp nhanh), độ phức tạp của thuật toán Quick Sort sẽ là O(n^2). Tại thời điểm đó, mảng không được chia thành bất kỳ phần nào cả, 2 bài toán con lần lượt có kích thước là n-1 và 0.
- Với phân đoạn hoàn hảo: Mỗi bài toán con có kích thước là n/2. Mảng cũng được phân thành hai phần bằng nhau. Độ phức tạp lúc này là O(nlogn).
- Với phân đoạn cân bằng: Một bài toán con có kích thước là n-k, bài còn lại có kích thước là k. Độ phức tạp lúc này là O(n).
>>> Xem thêm:
Kết luận
Thông qua bài viết trên, Teky đã giúp bạn đọc hiểu thêm về thuật toán Quick Sort trong Java. Mong rằng bạn đọc đã nắm rõ được những thông tin cơ bản xoay quanh thuật toán này. Chúc bạn nhanh gọn ứng dụng được Quicksort Java vào trong việc làm của mình .
tin tức nên biết Học Viện Công Nghệ Teky
TEKY là Học viện sáng tạo công nghệ với chương trình giảng dạy STEAM (Science – Technology – Engineering – Art – Mathematics) theo chuẩn Mỹ đầu tiên tại Việt Nam dành cho trẻ em từ 4 đến 18 tuổi.
Được xây dựng vào tháng 6 năm năm nay, TEKY quyết tâm thực thi thiên chức mang đến cho thế hệ trẻ Nước Ta kỹ năng và kiến thức tổng lực về STEAM, đặc biệt quan trọng là các tư duy công nghệ tiên tiến, khoa học máy tính và kiến thức và kỹ năng thế kỷ 21 – 4C s ( Critical Thinking : Tư duy phản biện – Communication : Giao tiếp – Creativity : Sáng tạo – Collaboration : Làm việc nhóm ) .
Đây là chương trình không chỉ trang bị kiến thức và kỹ năng lập trình mà còn rèn luyện nhóm kiến thức và kỹ năng 4C s. Trẻ sẽ được :
Các bộ môn giảng dạy tại Teky gồm : Lập trình và tăng trưởng ứng dụng, lập trình game, lập trình web với python Lập trình Scratch Robotics Engineering, Công nghệ 3D và MultiMedia. Chúng tôi tin rằng trẻ nhỏ Nước Ta có thời cơ tăng trưởng can đảm và mạnh mẽ trong một nền kinh tế tài chính số và cần được trang bị sẵn sàng chuẩn bị để trở thành những người kinh doanh công nghệ tiên tiến trong tương lai .
Liên hệ ngay học viện công nghệ sáng tạo TEKY để được tư vấn khóa học:
- Cam kêt 7 tuổi hoàn toàn có thể lập trình
- Top 10 dự án Bất Động Sản giáo dục có tầm tác động ảnh hưởng nhất Khu vực Đông Nam Á 2017 và 2018
-
Top 3 Dự án xuất sắc nhất, NextGen – Thụy Sĩ
Xem thêm: HashSet trong Java – Freetuts
- hotline Thành Phố Hà Nội : 024-7109-6668 | 0975-241-015
- đường dây nóng Hồ Chí Minh : 028 – 7109 9948 | 097-900-8642
Website https://final-blade.com | E-Mail : [email protected] |
Source: https://final-blade.com
Category: Kiến thức Internet