Tin Học PyThon 11 - Bài 6: Phép Toán, Biểu Thức, Câu Lệnh Gán 12/2022

Tóm Tắt

Danh sách bài học

Video hướng dẫn

Mục tiêu bài học:

Biết các khái niệm: Phép toán, biểu thức số học, hàm số học chuẩn, biểu thức quan hệ,..
Hiểu lệnh gán.
Viết được lệnh gán.
Viết được các biểu thức số học và logic với phép toán thông dụng.

1. Các phép toán

a. Các phép toán số học với số nguyên

Phép toán	Kí hiệu	Ví dụ
Cộng	+	2 + 1 = 3
Trừ	–	2 – 1 = 1
Nhân	*	2 * 1 = 2
Lũy thừa	**	2 ** 2 = 4
Chia	/	2 / 2 = 1
Chia lấy thương	//	3 // 2 = 1
Chia lấy dư	%	3 % 2 = 1

Ví dụ 1:

Chương trình:

import math
x = 4
y = 10
print(“Tổng của hai số là: “,x+y)
print(“Tích của hai số là: “,x*y)

Bạn đang đọc: Tin Học PyThon 11 – Bài 6: Phép Toán, Biểu Thức, Câu Lệnh Gán 12/2022

hình tính tổng và tích của 2 số

Kết quả:

kết quả tính tổng và tích của hai số

Ví dụ 2: Viết chương trình tính trung bình cộng 3 số nguyên dương x,y,z. Hiển thị giá trị TBC ra màn hình.

Chương trình:

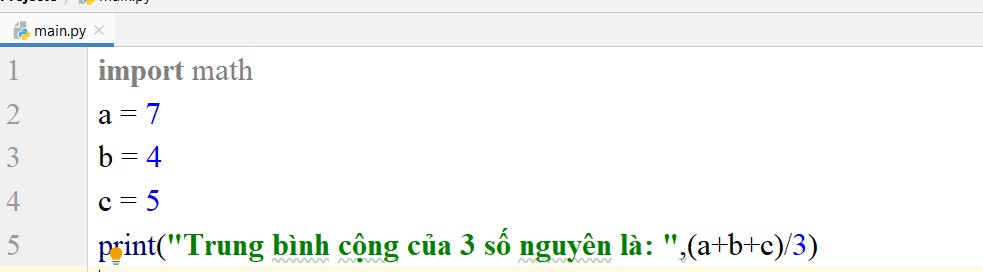
import math
a = 7
b = 4
c = 5
print(“Trung bình cộng của 3 số nguyên là: “,(a+b+c)/3)

hình tính giá trị trung bình cộng 3 số nguyên Kết quả:

Python cho phép đo lường và thống kê với những số nguyên có giá trị lớn .
Ví dụ :
Hiển thị hiệu quả 2021 lũy thừa 20 :

Chương trình:

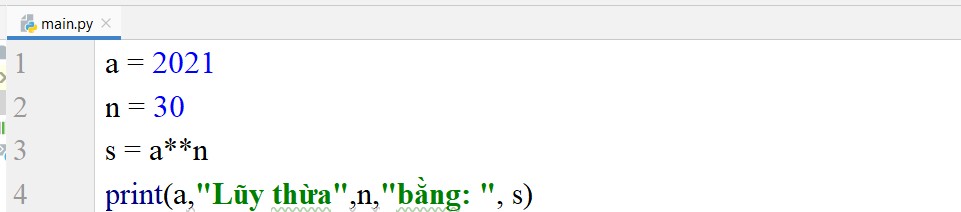
a = 2021
n = 20
s = a**n
print(a,”Lũy thừa”,n,”bằng: “, s)

Kết quả trả về sẽ là : 2021 lũy thừa 20 bằng :
1292189686118758098157753139519670145272740985698542594558228436401

hình ảnh tính lũy thừa số nguyên Kết quả:

kết quả tính lũy thừa số nguyên

b. Các phép toán số học với số thực

Phép toán	Ký hiệu	Ví dụ
Cộng	+	2.0 + 1.0 = 3.0
Trừ	–	3.0 – 1.0 = 2.0
Nhân	*	4.0 * 2.0 = 8.0
Lũy thừa	**	4.0 ** 2.0 = 16.0
Chia	/	4.0 / 2.0 = 2.0

Ví dụ : Viết chương trình tính chu vi hình tròn trụ biết nửa đường kính r = 5. Hiển thị giá trị chu vi ra màn hình hiển thị .

Chương trình:

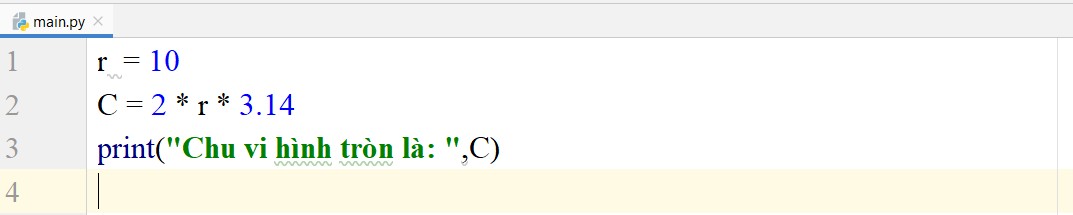
r = 10
C = 2 * r * 3.14
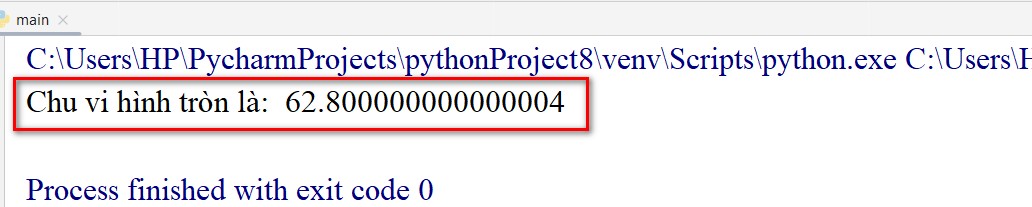
print(“Chu vi hình tròn là: “,C)

hình ảnh tính chu vi hình tròn

Kết quả:

c. Các phép toán quan hệ

Phép toán	Ký hiệu	Ví dụ
Lớn hơn	>	a > b
Nhỏ hơn	<	a < b
Bằng	==	a == b
Khác	!=	a != b
Lớn hơn hoặc bằng	>=	a >= b
Nhỏ hơn hoặc bằng	<=	a <= b

Chú ý : Kết quả của những phép toán quan hện cho giá trị logic ( True or False ) .

d. Các phép toán logic

Phép toán	Ký hiệu	Ví dụ
True khi cả hai đều True	and	a and b
True nếu một trong hai là True	or	a or b
Không True khi False	not	not a

Chú ý : Một trong những ứng dụng của phép toán logic là để tạo ra những biểu thức phức tạp từ những quan hệ đơn thuần .

2. Các biểu thức

a. Biểu thức số học

Biểu thức số học là một biến kiểu số hoặc một hằng số hoặc những biến kiểu số và những hằng số được link với nhau bởi phép toán số học, những dấu ngoặc tròn ( và ) tạo thành một biểu thức số học .
Quy tắc viết biểu thức số học trong lập trình :

Chỉ dùng cặp ngoặc tròn () để xác định trình tự thực hiện.
Viết lần lượt từ trái qua phải.
Không được bỏ qua dấu nhân trong tích.

Thứ tự thực hiện các phép toán:

Thực hiện các phép toán trong ngoặc trước.
Thực hiện từ trái sang phải.
Các phép toán: *,/,//,% thực hiện trước; các phép toán +, – thực hiện sau.

Ví dụ:

Biểu thức trong toán học	Biểu thức trong Python
2x + y	2*x + y
7a – (3b2-5a)	7a – (3a2 – 5a)
ab/(4-3a)	ab/(4 – 3a)
4a^2-(2+4ab)^2	4aa – (2 + 4ab)(2 + 4a*b)

b. Biểu thức quan hệ

Biểu thức quan hệ là hai biểu thức cùng kiểu link với nhau bởi phép toán quan hệ .

Biểu thức 1, biểu thức 2 cùng là xâu, hoặc cùng là biểu thức số học .

Thứ tự thực hiện:

Bước 1: Tính giá trị các biểu thức.

Bước 2: Thực hiện phép toán quan hệ.

Biểu thức quan hệ	Giá trị tham chiếu	Thực hiện phép toán quan hệ
a + 20 > 23	a = 4	4 + 20 > 23
(5^X – 3) > 10	X = 2	(5^2 – 3) > 10

Kết quả của biểu thức quan hệ kiểu logic .

c. Biểu thức logic

Biểu thức logic là những biểu thức logic đơn thuần, những biểu thức quan hệ link với nhau bởi phép toán logic .

Xem thêm: Aliases là gì? Hướng dẫn cấu hình Alias domain trong Cpanel – Trung tâm hỗ trợ kỹ thuật | MATBAO.NET

Biểu thức logic đơn thuần là biến logic hoặc hằng logic .
Các biểu thức quan hệ phải được đặt trong cặp dấu ( ) .

Thứ tự thực hiện:

Bước 1: Tính giá trị các biểu thức.

Bước 2: Thực hiện phép toán logic.

Biểu thức logic	Giá trị tham chiếu	Kết quả
not ( a > 5 )	a = 6	F
(a > 10) and (X < 9)	a = 11, X = 8	T
(a == 5) or (b > 9)	a = 3, b = 10	T

Kết quả của biểu thức logic thuộc kiểu logic .

3. Hàm số học chuẩn

Một số hàm chuẩn thường dùng trong Python:

Toán học	Python
Hàm bình phương: x^2	x**2
Hàm căn bậc hai: √ x	sqrt(x)
Hàm giá trị tuyệt đối: \|x\|	abs(x)
Hàm logarit tự nhiên: ln(x)	log(x)
Hàm lũy thừa của cơ số e: e^x	exp(x)
Hàm sin: sin(x)	sin(x)
Hàm cos: cos(x)	cos(x)

Trong Python, những hàm số học chuẩn này được định nghĩa trong module math. Để sử dụng những hàm nay trong Python, tất cả chúng ta cần thực thi hàm import math ( trừ những hàm : abs ( ), x * * 2 .
Ví dụ : Trước khi sử dụng những hàm toán học ví dụ : sqrt ( ), … thì bạn phải sử dụng thư viện math và kèm theo math. hàm toán học .

Chương trình:

import math
a = 5
b = math.sqrt(a)
print(b)

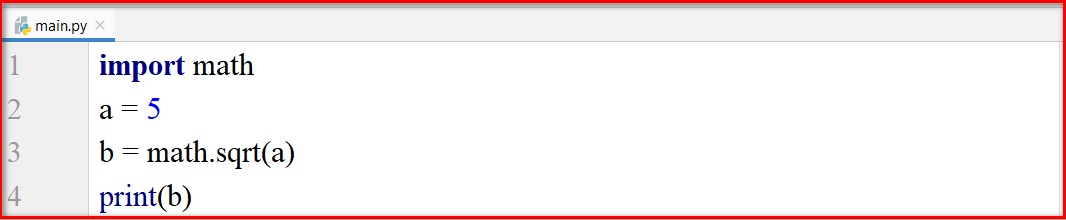
hình sử dụng hàm toán học

Kết quả:

kết quả sử dụng hàm toán học

Ví dụ trường hợp không sử dụng thư viện math :

Chương trình:

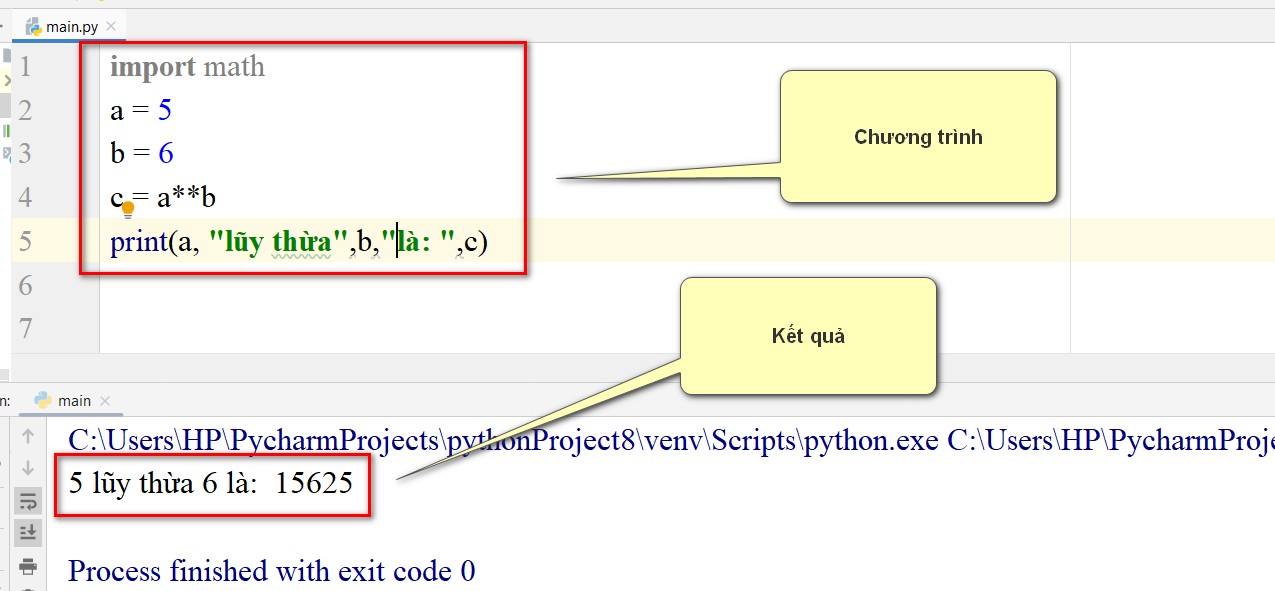
import math
a = 5
b = 6
c = a**b
print(a, “lũy thừa”,b,”là: “,c)

hình chương trình không cần sử dụng hàm toán học

Ví dụ 2: Biểu diễn biểu thức -b + (√(b^2 )-4*a*c)/(2*a*c)

sang biểu thức trong ngôn từ lập trình Python :

(-b + sqrt(b**2-4*a*c))/(2*a*c)

Ví dụ 3: Biểu diễn biểu thức: abs(x-y)/(x**2 + sqrt(y) + 1 sang biểu thức trong toán học:

| x-y | / ( x ^ 2 + √ y + 1 )

4. Câu lệnh gán

Câu lệnh gán trong Python dùng dấu = để gán giá trị bên phải cho biến bên trái.

Các lệnh gán trong Python cụ thể như sau:

Toán tử	Ví dụ	Tương đương với
=	x = 3	x = 3
+=	a +=9	a = a + 9
-=	a -=10	a = a – 10
*=	a *= 2	a = a * 2
/=	a /=3	a = a/3
%=	a %=2	a = a%2
//=	a //= 3	a = a//3
**=	x **= 1	a = a ** 1