Độ phức tạp thời gian BigO là gì?

Ở bài học kinh nghiệm này, tất cả chúng ta sẽ cùng nhau tìm hiểu và khám phá một yếu tố sẽ theo tất cả chúng ta xuyên suốt khóa học này – độ phức tạp thời hạn BigO. Đây là thứ sẽ cho tất cả chúng ta biết một thuật toán hoặc cấu trúc tài liệu thực thi nhanh hay chậm .

Tóm Tắt

Nội dung

Để hoàn toàn có thể hiểu được bài học kinh nghiệm này một cách tốt nhất, những bạn nên có kiến thức và kỹ năng cơ bản về những phần :

Trong bài học này chúng ta sẽ tìm hiểu về:

Bạn đang đọc: Độ phức tạp thời gian BigO là gì? | How Kteam

Khái niệm thời gian chạy của chương trình
Khái niệm về độ phức tạp thời gian
Cách đánh giá độ phức tạp của thuật toán

Khái niệm thời gian chạy của chương trình

Thời gian chạy của chương trình
là quãng thời gian mà máy tính cần để thực hiện toàn bộ những yêu cầu mà người dùng đặt ra.

Cùng tìm hiểu thêm ví dụ sau :

#include
using namespace std;
 
int main(){
for (int i = 0 ; i < 100 ; ++i){
   cout << "Kteam" << endl;
} 
return 0 ; 
}

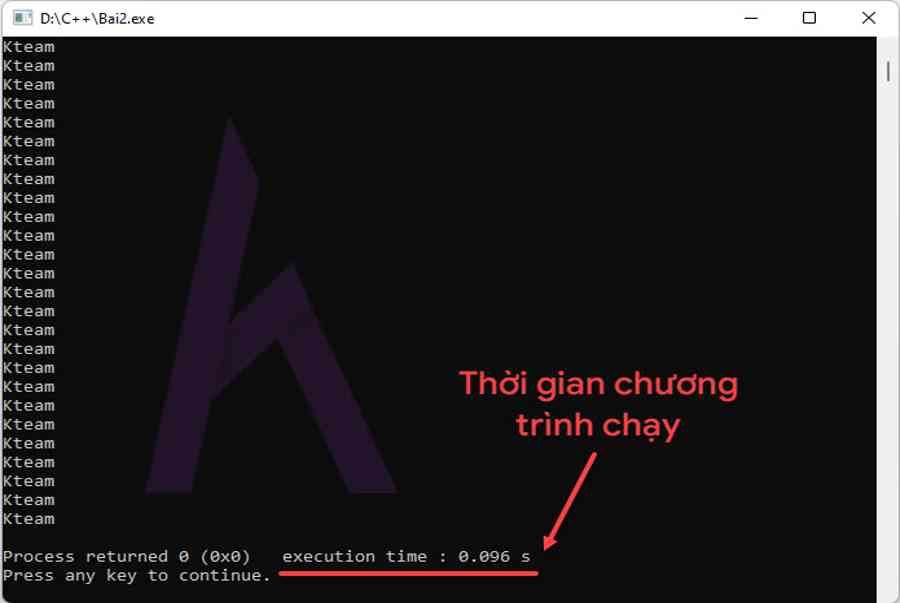
Kết quả:

Kết quả ví dụ thời gian chạy chương trình Howkteam.vn

Ở ví dụ trên, ta có thể thấy: thời gian mà chương trình chạy đó là 0.096s.

Câu hỏi đặt ra là: Không
nhẽ cứ mỗi lần chúng ta muốn biết được xem liệu chương trình, thuật toán mà ta định viết nhanh hay chậm ta lại phải code thử rồi chạy để xem thời gian sao?

Cách này sẽ có một số ít điểm yếu kém sau :

Cùng một đoạn code, nếu như được thực thi trên
hai máy khác nhau có thể cho ra các kết quả khác nhau
về thời gian chạy
Đối với các chương trình nhận dữ liệu đầu vào, sẽ có
sự khác nhau về thời gian chạy do sự khác biệt về dữ liệu
Tốn thời gian cài đặt chương trình

Vậy thì làm thế nào để hoàn toàn có thể ước đạt thời hạn chạy của chương trình cũng như so sánh thời hạn chạy những thuật toán, những cấu trúc tài liệu với nhau ?
Đó chính là lúc tất cả chúng ta cần đến việc nhìn nhận độ phức tạp thời hạn .

Khái niệm về độ phức tạp thời gian

Độ phức tạp thời gian

Độ phức tạp thời gian là toàn bộ tài nguyên về thời gian mà máy tính cần để thực thi một thuật toán nào đó, được thể hiện bằng hàm số $y = f\left ( x \right )$ .
Thông thường, độ phức tạp thời gian sẽ dựa vào số lần mà một câu lệnh cơ bản với thời gian thực thi là hằng số được thực thi. Chúng ta sẽ tìm hiểu rõ hơn qua ví dụ ở các phần sau.

Đối với một chương trình, sẽ có hai loại độ phức tạp là độ phức tạp thời gian và
độ phức tạp bộ nhớ. Tuy nhiên, trong khoá học này, mình sẽ chủ yếu đề cập đến
độ phức tạp thời gian. Do đó, khi mình nói “độ phức tạp chương trình” tức là nói về độ phức tạp thời gian của chương trình đó.

Trên thực tế, do sự khác biệt về dữ liệu đầu vào như đã nói ở trên, đa phần các thuật toán sẽ được tính toán độ phức tạp dựa vào trường hợp xấu nhất
(worst-case), tức là khoảng thời gian tối đa mà chương trình sẽ chạy với một bộ dữ liệu có kích thước cố định. Một số thuật toán sẽ được đánh giá dựa theo trường hợp trung bình
(average-case) ví dụ như Quick Sort. Để biết tại sao Quick Sort lại được đánh giá dựa vào trường hợp trung bình thì hãy tiếp tục theo dõi khoá học này nhé.
Ngoài ra còn có một cách đánh giá dựa vào trường hợp tốt nhất
(best-case). Tuy nhiên, ta sẽ không quan tâm đến cách đánh giá này do nó không bao giờ được áp dụng trong thực tế.

Tuy nhiên, do các hàm số thể hiện độ phức tạp thường rất khó tính toán nên chúng ta cần một phương pháp đánh giá hiệu quả hơn. Một cách được sử dụng phổ biến đó là
Độ phức tạp thời gian BigO.

Độ phức tạp thời gian BigO

Độ phức tạp thời gian BigO
(Big O notation) thể hiện sự thay đổi của độ phức tạp thời gian phụ thuộc vào sự thay đổi của dữ liệu đầu vào.

Đồ thị minh họa Big O Howkteam.vn

Ở bên trên, chúng ta có một đồ thị minh hoạ sự phụ thuộc của
số lệnh cơ bản được thực thi (N) trục Oy vào
kích thước dữ liệu đầu vào (n) trục Ox. Vậy sự phụ thuộc này chính xác là như thế nào thì chúng ta hãy cùng tìm hiểu về một số độ phức tạp thời gian cơ bản ở tiếp theo.

Một số độ phức tạp thời gian cơ bản

Có rất nhiều độ phức tạp thời hạn và trong bài này Kteam sẽ ra mắt đến bạn một số ít độ phức tạp cơ bản. Từ đó, bạn trọn vẹn hoàn toàn có thể dựa trên những gì mình đã trình diễn để suy ra những độ phức tạp khác .

TÊN	ĐỊNH NGHĨA	VÍ DỤ
Độ phức tạp hằng số O(1)	Một thuật toán được gọi là có độ phức tạp hằng số O(1) khi thời gian chạy không phụ thuộc vào kích thước dữ liệu đầu vào.	những toán tử cơ bản, truy vấn vào một thành phần của mảng, in ra 1 xâu, …
Độ phức tạp tuyến tính O(n)	Một thuật toán được gọi là có độ phức tạp tuyến tính O(n) khi thời gian chạy thay đổi tuyến tính phụ thuộc vào kích thước dữ liệu đầu vào.	Kích thước tài liệu nguồn vào là 10, thời hạn chạy mất 1 s. Khi size tài liệu nguồn vào là 100, thời hạn chạy mất 10 s thì khi đó ta nói thuật toán có độ phức tạp O ( n ) .
Độ phức tạp theo hàm số logarit O(log n)	Một thuật toán được gọi là có độ phức tạp theo hàm số logarit O(log n) khi thời gian chạy thay đổi theo dạng hàm số logarit phụ thuộc vào kích thước dữ liệu đầu vào. Xem thêm: Trí Tuệ Nhân Tạo AI là gì?	tìm kiếm nhị phân, các thao tác với cây nhị phân, …

Chú ý:

Khi ta nói độ phức tạp của thuật toán là O(log n) thì log n ở đây không phải là log10 n như trong Toán học. Trên thực tế, với tất cả các hàm logarit có cơ số lớn hơn 1, chúng đều tiệm
cận nhau, do đó chúng ta sẽ nói chung là log n kể cả khi khác cơ số.

Sẽ có những lúc tồn tại hàm O(k * n)
với hằng số k. Thực chất, viết như vậy ta vẫn sẽ hiểu độ phức tạp tăng tuyến tính với n. Việc viết thêm k vào giúp ta có đánh giá chính xác hơn về độ phức tạp thuật toán. Tuy nhiên, ta chỉ quan tâm đến hằng số k khi k thật sự có một ảnh hưởng lớn lên độ phức
tạp bài toán. Với đa số thuật toán, k là

không đáng kể

.

Khi so sánh các thuật toán bằng cách đánh giá độ phức tạp thời gian BigO thì kết quả sẽ chỉ là
tương đối. Hai thuật toán có cùng độ phức tạp có thể có số câu lệnh cơ bản khác nhau dẫn đến thời gian chạy sẽ khác nhau (Lí do là do hằng số k được nêu ở trên).

Cách đánh giá độ phức tạp của thuật toán

Quy tắc

Đối với lập trình thi đấu, thường khi ta nói “một thuật toán có độ phức tạp O(A)” có nghĩa là có tối đa A câu lệnh O(1) được thực thi. Việc đánh giá độ phức tạp chính là tính số lần thực thi tối
đa của một câu lệnh O(1).

Để nhìn nhận độ phức tạp của một thuật toán không đệ quy hoàn toàn có thể tóm gọn lại như sau :

Tính số lần lặp tối đa của một vòng lặp
Nếu các vòng lặp nối tiếp nhau thì cộng số lần lặp tối đa của các vòng lặp với nhau
Nếu các vòng lặp lồng nhau thì nhân số lần lặp tối đa của các vòng lặp với nhau

Chúng ta sẽ đi qua một số ít ví dụ để những bạn hoàn toàn có thể hiểu hơn về cách nhìn nhận một thuật toán trong trong thực tiễn

Ví dụ 1: Phụ thuộc vào giá trị n

Yêu cầu : In ra dòng chữ “ Kteam ” với số lần phụ thuộc vào vào giá trị n nhập từ bàn phím .

using namespace std;
 
int n;
 
int main(){
    cin >> n;
    for(int i = 0 ; i < n ; ++i){ 
       cout << "Kteam" << endl;
    }
    return 0;
}

Từ đoạn code trên, ta hoàn toàn có thể thấy :

L
ệnh in ra dòng chữ “Kteam” là một lệnh có độ phức tạp hằng số
O(1).
Vòng lặp này lặp lại tối đa n lần. Do đó, theo quy tắc 1 ở trên ta sẽ có độ phức tạp vòng lặp là O(1 * n) hay là
O(n)

Ví dụ 2: Phụ thuộc vào giá trị n và m

Yêu cầu : In ra dòng chữ “ Kteam ” với số lần nhờ vào vào giá trị n và m nhập từ bàn phím .

#include
using namespace std;
 
int n, m;
 
int main(){
    cin >> n >> m;
    for(int i = 0 ; i < n ; ++i){
        for(int j = 0 ; j < m ; ++j){
           cout << "Kteam" << endl;
        }
    }
 
    return 0;
}

Ở đoạn code phía trên, tất cả chúng ta thấy có :

Một vòng for lặp m lần in ra dòng chữ “Kteam”. Do đó độ phức tạp của vòng for sẽ là
O(m) như ví dụ 1.
Vòng for j lại được lồng trong vòng for i lặp lại
n lần. Do đó theo quy tắc 2, độ phức tạp hai vòng for này là
O(n * m)

Ví dụ 3

Yêu cầu : In ra dòng chữ “ Kteam ” với số lần nhờ vào vào giá trị n và m nhập từ bàn phím, tựa như ví dụ 2 .

#include
using namespace std;
 
int n, m;
 
int main(){
    cin >> n >> m;
    for(int i = 0 ; i < n ; ++i){ 
        cout << "Kteam" << endl;
    }    
    for(int i = 0 ; i < n ; ++i){
        for(int j = 0 ; j < m ; ++j){
            cout << "Kteam" << endl;
        }
    }
 
    return 0;
}

Ví dụ này được gộp từ yêu cầu của hai ví dụ trên. Theo quy tắc 3, hẳn bạn cũng đã đoán được độ phức tạp là O(n + n * m) đúng không?

Thực tế thì đáp án này không sai, nhưng do sự khác biệt giữa
O(n * m) và O(n + n * m) là không quá lớn
nên để đơn giản ta sẽ nói chương trình có độ phức tạp O(n * m).

Trong thực tế khi đánh giá một thuật toán cũng sẽ như vậy. Khi một phép toán ảnh hưởng không lớn đến thời gian chạy tổng thể của chương trình thì ta sẽ bỏ qua nó. Ở các ví dụ trên, bản thân câu lệnh
cin cũng mất thời gian
O(1). Tuy nhiên do ảnh hưởng của câu lệnh lên độ phức tạp thời gian chung là không đáng kể nên ta sẽ bỏ qua.

Vậy bạn có tự hỏi với các câu lệnh, toán tử, hàm, … có sẵn trong C++ (tức là các yếu tố không phải do chúng ta tạo ra) thì làm sao để biết độ phức tạp của nó là bao nhiêu?

Để lại quan điểm của bạn dưới phần phản hồi để cùng đàm đạo với mọi người nhé !

Kết luận

Qua bài này tất cả chúng ta đã nắm được độ phức tạp thời hạn và cách nhìn nhận độ phức tạp thời hạn của chương trình .

Bài sau chúng ta sẽ bắt đầu tìm hiểu về Cấu trúc dữ liệu Stack.

Xem thêm: Năm mới – Học ngôn ngữ mới, 8 cách để thực hiện điều đó ‹ GO Blog | EF Blog Vietnam

Cảm ơn các bạn đã theo dõi bài viết. Hãy để lại bình luận hoặc góp ý của mình để phát triển bài viết tốt hơn. Đừng quên “Luyện tập – Thử thách – Không ngại khó”.

Thảo luận

Nếu bạn có bất kể khó khăn vất vả hay vướng mắc gì về khóa học, đừng ngần ngại đặt câu hỏi trong phần bên dưới hoặc trong mục HỎI và ĐÁP trên thư viện Howkteam. com để nhận được sự tương hỗ từ hội đồng .

Source: https://final-blade.com
Category : Kiến thức Internet

admin

final-blade.com