Kiểu dữ liệu số trong Python | How Kteam

Dẫn nhập

Trong các bài trước, bạn đã làm quen với khái niệm BIẾN TRONG PYTHON .

Ở bài này Kteam sẽ đề cập đến các bạn KIỂU DỮ LIỆU SỐ. Một trong những kiểu dữ liệu cực kì quan trọng của Python!

Nội dung chính

Để đọc hiểu bài này tốt nhất bạn cần:

Bạn đang đọc: Kiểu dữ liệu số trong Python | How Kteam

Trong bài học kinh nghiệm này, tất cả chúng ta sẽ cùng tìm hiểu và khám phá các yếu tố :

Số là gì?
Một số kiểu dữ liệu số cơ bản trong Python.
Các toán tử cơ bản với kiểu dữ liệu số trong Python.
Thư viện math trong Python.

Số là gì?

Con số ở khắp nơi trong đời sống tất cả chúng ta. Bất cứ khi nào bạn cũng hoàn toàn có thể phát hiện số lượng trong đời sống .
Tháng này có 30 hay 31 ngày ? Mai đi chợ bó rau muốn 3000 đồng hay là 3500 đồng ? Bài thi hôm bữa được 9,1 điểm hay là 1,9 ? Cái bánh này mình ăn ½ hay là ¾. Có thể thấy, số không còn là điều gì lạ lẫm với bạn. Và đương nhiên điều này tựa như với “ con trăn ” Python .
Trong Python cũng tương hỗ rất nhiều kiểu dữ liệu số. Một số kiểu dữ liệu cơ bản như số nguyên ( integers ), số thực ( floating-point ), phân số ( fraction ), số phức ( complex ). Và những kiểu dữ liệu này sẽ được Kteam ra mắt cho các bạn ngay sau đây !

Một số kiểu dữ liệu số cơ bản trong Python

Số nguyên

Số nguyên bao gồm các số nguyên dương (1, 2, 3, ..), các số nguyên âm (-1, -2, -3) và số 0. Trong Python, kiểu dữ liệu số nguyên cũng không có gì khác biệt.

Ví dụ: Gán giá trị cho một biến a là 4 và xuất ra kiểu dữ liệu của a.

>>> a = 4    # gán giá giá trị của biến a là số 4, là một số nguyên
>>> a
4
>>> type(a)  # số nguyên thuộc lớp ‘int’ trong Python

Một điểm đáng quan tâm trong Python 3. X đó là kiểu dữ liệu số nguyên là vô hạn. Điều này được cho phép bạn đo lường và thống kê với những số cực kỳ lớn, điều mà hầu hết các ngôn từ lập trình khác KHÔNG THỂ .

Số thực

Về kiểu dữ liệu số thực, thì đây là tập hợp các số nguyên và số thập phân 1, 1.4, -123, 69.96,…

Ví dụ: Gán giá trị của biến f là 1.23 và xuất ra kiểu dữ liệu của f.

>>> f = 1.23   # gán giá trị của biến f là số 1.23, là một số thực
>>> f
1.23
>>> type(f)    # số thực trong Python thuộc lớp ‘float’

>>> q = 1.0   # đây là số thực, không phải số nguyên
>>> q
1.0
>>> type(q)

Lưu ý: Thường khi chúng ta viết số thực, phần nguyên và phần thập phân được tách nhau bởi dấu phẩy (, ). Thế nhưng trong Python, dấu phẩy (, ) này được thay thế thành dấu chấm (. )

Số thực trong Python có độ đúng chuẩn xê dịch 15 chữ số phần thập phân .

Ví dụ: Số thực 10/3

>>> 10 / 3   # đây là một số vô hạn tuần hoàn 3.3333333333333333333..
3.3333333333333335

Nếu bạn muốn có kết quả được chính xác cao hơn, bạn nên sử dụng
Decimal

>>> from fractions import Fraction   # lấy toàn bộ nội dung của thư viện Decimal,khuyến khích dùng: from fractions import Fraction trong việc học để tạo thói quen trong công việc sau này.
>>> getcontext().prec = 30   # lấy tối đa 30 chữ số phần nguyên và phần thập phân Decimal
>>> Decimal(10) / Decimal(3)
Decimal(‘3. 33333333333333333333333333333’)
>>> Decimal(100) / Decimal(3)
Decimal(’33.3333333333333333333333333333’)
>>> type(Decimal(5))   # các số Decimal thuộc lớp Decimal

Tuy Decimal có độ đúng chuẩn cao hơn so với float tuy nhiên nó lại khá rườm rà so với float. Do đó, hãy cân đối sự thuận tiện và đúng chuẩn để chọn kiểu dữ liệu tương thích .

Phân số

Chúng ta biết đến phân số qua sách giáo khoa toán lớp 3. Phân số gồm hai phần là
tử số và mẫu số.

Tạo một phân số

Để tạo phân số trong python, ta sử dụng hàm Fraction với cú pháp sau

Fraction(, )

Ví dụ: Nhập phân số ¼, 3/9, ¾,

>>> from fractions import * # lấy toàn bộ nội dung của thư viện decimal
>>> Fraction(1, 4)   # phân số với tử số là 1, mẫu số là 4.
Fraction(1, 4)
>>> Fraction(3, 9)  # phân số sẽ được tối giản nếu có thể
Fraction(1, 3)
>>> type(Fraction(3, 4))  # các phân số thuộc lớp Fraction

Tất nhiên, việc tạo một phân số với mẫu số bằng 0 sẽ gây lỗi .

>>> from fractions import *
>>> Fraction(1, 0)
Traceback (most recent call last):
  File "", line 1, in 
  File "C:\Users\PC\AppData\Local\Programs\Python\Python310\lib\fractions.py", line 156, in __new__
    raise ZeroDivisionError('Fraction(%s, 0)' % numerator)
ZeroDivisionError: Fraction(1, 0)
>>> Fraction(1.55, 0)
Traceback (most recent call last):
  File "", line 1, in 
  File "C:\Users\PC\AppData\Local\Programs\Python\Python310\lib\fractions.py", line 152, in __new__
    raise TypeError("both arguments should be "
TypeError: both arguments should be Rational instances

Số phức

Nếu bạn chưa biết đến Số Phức, Kteam khuyên bạn nên bỏ qua phần này.

Số phức gồm 2 thành phần :

+ j

Trong đó

là số thực
j là đơn vị ảo trong toán học với j2 = -1

Tạo một số phức

Để tạo một số phức, bạn có thể sử dụng hàm complex với cú pháp sau

complex(,)

Gán giá trị số phức cho một biến

= + j

Xuất ra từng phần của một biến số phức

Để xuất ra phần thực, ta sử dụng cú pháp :

.real

Để xuất ra phần ảo của biến số phức, ta dùng cú pháp :

.imag

Ví dụ: Nhập một số số phức sau

1 + 3j
Gán biến c có giá trị 2+1j. Xuất ra phần thực và phần ảo của biến c.
4 +j (sẽ có lỗi vì kiểu dữ liệu nhập vào không đúng).
Tạo số phức có phần thực là 3, phần ảo là 1.
Tạo số phức chỉ có phần thực là 2.
Xuất ra kiểu dữ liệu của số 3+1j.

>>> 3j + 1  # phần thực là 1, phần ảo là 3
(1 + 3j)
>>> c = 2 + 1j  # gán giá trị cho biến c là một số phức với phần thực là 2 còn phần ảo là 1
>>> c
(2 + 1j)
>>> 4 + j   # phần ảo là 1, tuy vậy chúng ta không được phép bỏ số 1 như trong toán
Traceback (most recent call last):
  File "", line 1, in 
NameError: name 'j' is not defined
>>> 4 + 1j
(4 + 1j)
>>> c.imag  # lấy phần ảo của số phức 2 + 1j mà ta đã gán cho biến c
1.0
>>> c.real  # lấy phần thực
2.0
>>> complex(3, 1)  # dùng hàm complex để tạo một số phức với phần thực là 3, ảo là 1
(3 + 1j)
>>> complex(2)      # chỉ có phần thực, phần ảo được mặc định là 0
(2 + 0j)
>>> type(3 + 1j)   # các số phức thuộc lớp complex

Các toán tử cơ bản với kiểu dữ liệu số trong Python

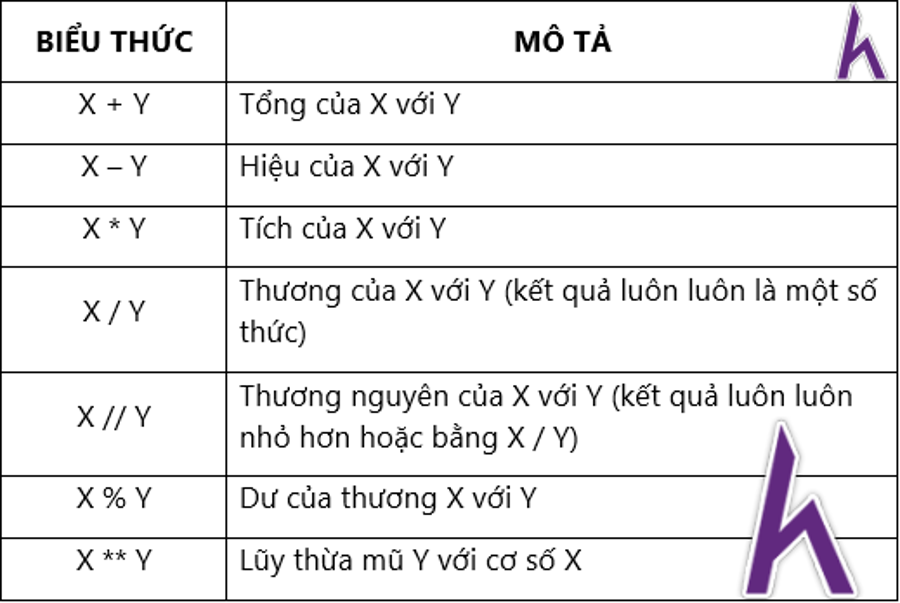
Biểu thức chính là một thực thể toán học. Nói cách khác, nó là một sự kết hợp giữa 2 thành phần:

Toán hạng: có thể là một hằng số, biến số (X, Y)
Toán tử: xác định cách thức làm việc giữa các toán hạng (+,-,*,/)

Dưới đây là một số ít biểu thức toán học của kiểu dữ liệu số trong Python

Kiểu dữ liệu số trong Python

Ví dụ: Cho 2 biến a,b lần lượt bằng 8 và 3. Thực hiện các biểu thức toán học với a,b.

>>> a = 8
>>> b = 3
>>> a + b   # tương đương 8 cộng 3
11
>>> a – b    # tương đương 8 trừ 3
5
>>> a * b   # tương đương 8 nhân 3
24
>>> a / b   # tương đương 8 chia 3
2.6666666666666665
>>> a // b  # tương đương với 8 chia nguyên 3
2
>>> a % b   # tương đương với 8 chia dư 3
2
>>> a ** b   # tương đương 8 mũ 3
512

Tránh nhầm lẫn khi thực hiện các phép tính với số thực (float)

Đôi lúc, ta thực hiện các phép tính với số thực, và kết quả trả về thật “mù mắt”:

Xem thêm: Top 10 phần mềm vẽ 3D chuyên nghiệp, tốt nhất hiện nay

>>> 0.1 + 0.2
0.30000000000000004
>>> 0.20 - 0.15
0.05000000000000002
>>> 0.05 * 0.2
0.010000000000000002

Không phải do lỗi của bạn, hay do python. Điều này xảy ra trên hàng loạt các ngôn từ lập trình. Một cách dễ hiểu, là cách tàng trữ số thập phân của máy tính tạo nên lỗi này .
Máy tính tàng trữ các số dưới dạng các dãy nhị phân. Do đó nên khi muốn tàng trữ bất kỳ 1 số ít nào đó, máy tính sẽ phải chuyển số đó về dạng nhị phân. Nhưng có nhiều số không hề được chuyển một cách đúng chuẩn trọn vẹn, và Open sai số .
Khi học tập cũng như khi thao tác, các bạn cần quan tâm đến những lỗi như thế này để tránh nhầm lẫn .

Mức độ ưu tiên của các toán tử

Kteam xin lưu ý cho các bạn khi sử dụng toán tử: Các phép toán được thực hiện từ bên trái sang phải của biểu thức, đồng thời có độ ưu tiên thực hiện khác nhau (giống như khi ta thực hiện các phép tính bình thường)
Bảng sau sẽ đề cập đến một số toán tử với độ ưu tiên thực hiện từ trên xuống dưới (các biểu thức được đặt trong cặp ngoặc đơn được tính toán đầu tiên):

Hãy cùng xem xét các ví dụ sau :

>>> 2 + 3 * 4 # Bằng 14 do phép nhân được thực hiện trước
14
>>> 2 * 3**2 # Bằng 18 do phép lũy thừa được thực hiện trước
18
>>> 2 * (2 + 3) – 3 # Bằng 7
7
>>> 2**3 * (1 + 3 % 2) # Bằng 16
16

Toán tử := (Assignment expression)

Nếu bạn để ý kĩ bảng trên, thì các bạn sẽ thấy một toán tử được gọi là
Assignment expression (kí hiệu :=) ở hàng cuối cùng. Tại sao nó lại được gọi với cái tên như vậy ? Công dụng của nó là gì ? Kteam sẽ giúp các bạn hiểu rõ hơn về toán tử này.

Thông thường, để gán giá trị cho một biến nào đó, ta dùng toán tử “ = ” ( phép gán ). Nhưng việc sử dụng nó cũng có những hạn chế. Hãy xem xét ví dụ sau :

>>> a = 1
>>> b = (a += 1) + 2
  File "", line 1
    b = (a += 1) + 2
           ^^
SyntaxError: invalid syntax
>>> b = 3
>>> print(b = 4)
Traceback (most recent call last):
  File "", line 1, in 
TypeError: 'b' is an invalid keyword argument for print()

Ta có thể thấy rằng, đối với toán tử “=”, việc gán các giá trị chỉ được thực hiện khi bản thân lệnh gán đó được dùng trên
một dòng. Việc thực hiện phép gán trong khi đang thực hiện các lệnh khác là
không được cho phép.

Toán tử “ : = ” được sinh ra là vì lí do đó. Nó giúp khắc phục được điểm yếu của toán tử “ = ” .
Mời các bạn cùng Kteam xem các ví dụ để hiểu rõ hơn :

>>> a = 3
>>> b = (a := a + 3) + 3 #Thay đổi giá trị của biến a, đồng thời khởi tạo biến b.
>>> a
6
>>> b
9
>>> print(c := 100) #Nếu cần, ta cũng có thể khởi tạo một biến bằng Assignment Expression
100
>>> (t := 4) #Việc khởi tạo biến bằng Assignment Expression bên ngoài lệnh cũng được cho phép, với điều kiện phép gán được đặt trong cặp ngoặc
4

So sánh giữa số với số trong Python

Bạn chắc biết so sánh là gì nhờ các tiết học toán ở trường. Ví dụ như

3 > 1 là đúng
69 < 10 là sai
241 = 141 + 100 là đúng
(5 x 0) ≠ 0 là sai.

Trong Python cũng có các toán tử như vậy. Tuy nhiên kí hiệu của chúng thì có khác đôi chút .
Bảng sau đây sẽ cho các bạn thông tin về những toán tử so sánh trong Python

Hãy xem ví dụ minh họa trong Python :

>>> 3 > 1 # 3 > 1 là đúng => True
True
>>> 69 < 10 # 69 < 10 là sai => False
False
>>> 241 == 141 + 100 # 241 = 141 + 100 là đúng => True
True
>>> (5 * 0) != 0  # 5 x 0 ≠ 0 là sai => False
False

Ngoài kiểu dữ liệu số, các toán tử so sánh còn hoàn toàn có thể được thực thi trên các kiểu dữ liệu khác – điều mà các bạn sẽ được tìm hiểu và khám phá trong các bài tiếp theo

Thư viện math trong Python

Thư viện math trong Python tương hỗ rất nhiều hàm giám sát tương quan đến toán học .
Để sử dụng một thư viện nào đó, ta dùng lệnh

import

Muốn sử dụng một hàm nào đó của thư viện, ta sử dụng cú pháp

.

Dưới đây là 1 số ít hàm thường được dùng trong việc giám sát cơ bản .

Kiểu dữ liệu số trong Python

Ví dụ:

>>> import math   # lấy nội dung của thư viện math về sử dụng
>>> math.trunc(3.9)
3
>>> math.fabs(-3)
3.0
>>> math.sqrt(16)
4.0
>>> math.gcd(6, 4)
2
>>> math.lcm(4, 5)
20
>>> >>> math.ceil(9.4)
10

Câu hỏi củng cố

Kiểu dữ liệu số nguyên thuộc lớp nào ?
Sự khác nhau giữa hai biến a và b dưới đây là gì ?

>>> a = 0
>>> b = 0.0

Tại sao lại có sự khác nhau khi sử dụng hàm `trunc` ở thư viện math so với toán tử `//`

>>> import math
>>> math.trunc(15 / -4)
-3
>>> 15 // -4
-4

Trong khi chúng lại có trùng tác dụng ở phép tính này .

>>> import math
>>> math.trunc(15 / 4)
3
>>> 15 // 4
3

Đáp án của phần này sẽ được trình diễn ở bài tiếp theo. Tuy nhiên, Kteam khuyến khích bạn tự vấn đáp các câu hỏi để củng cố kỹ năng và kiến thức cũng như thực hành thực tế một cách tốt nhất !

Bài tập trắc nghiệm rèn luyện Kquiz

Các bạn làm bài tập trắc nghiệm tại đây hoặc nhấn vào ảnh để giải đề .

Kết luận

Bài viết này đã ra mắt cho các bạn 1 số ít KIỂU DỮ LIỆU SỐ trong Python .

Ở bài sau, Kteam sẽ nói về
KIỂU DỮ LIỆU CHUỖI TRONG PYTHON – một kiểu dữ liệu cũng cực kì quan trọng.

Xem thêm: FreeShareVN”>Tải Hiren BootCD 15.2 Full-Hướng dẫn tạo USB Hiren Boot > FreeShareVN

Cảm ơn bạn đã theo dõi bài viết. Hãy để lại bình luận hoặc góp ý của mình để phát triển bài viết tốt hơn. Đừng quên “Luyện tập – Thử thách – Không ngại khó”.

Thảo luận

Nếu bạn có bất kể khó khăn vất vả hay vướng mắc gì về khóa học, đừng ngần ngại đặt câu hỏi trong phần bên dưới hoặc trong mục HỎI và ĐÁP trên thư viện Howkteam. com để nhận được sự tương hỗ từ hội đồng .

Source: https://final-blade.com
Category: Kiến thức Internet

admin

final-blade.com