Tóm Tắt
1. Số nguyên tố là gì ?
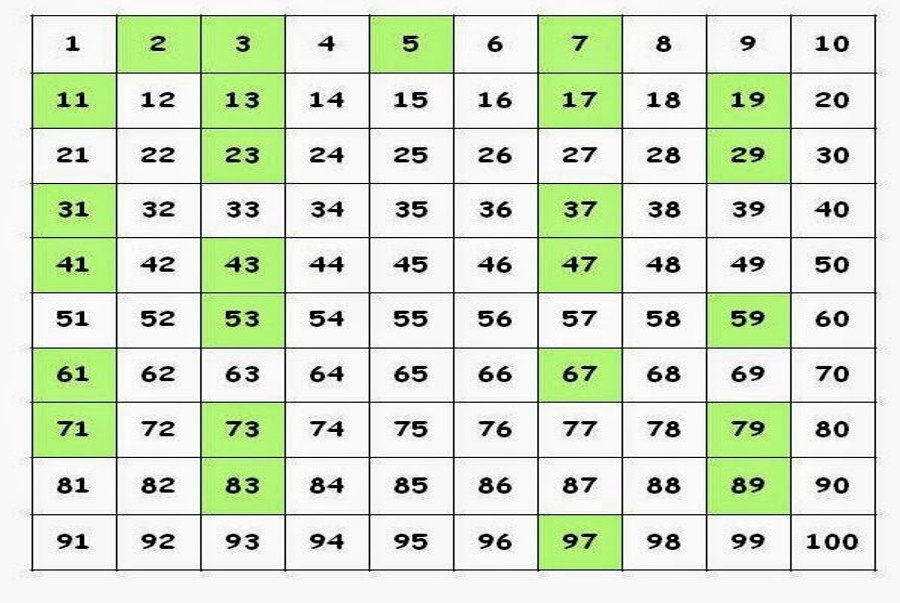
Số nguyên tố số chỉ chia hết cho 2 số 1 và chính nó. Có thể hiểu một cách đơn thuần, với một số ít tự nhiên lớn hơn 1, nếu ngoài chữ số 1 và bản thân chính số đó thì nó không chia hết cho số nào khác nữa. Ví dụ các số : 2, 3, 5, 7, 11, 13, 17, 23, 29, … đều được gọi là số nguyên tố .
Đặc biệt, có 2 trường hợp không được xét là nguyên tố đó chính là số 0 và số 1. Số 2 chỉ chia hết cho 1 và 2 nên 2 là số nguyên tố. Số 3 cũng chia hết cho 1 và 3 nên 3 là số nguyên tốt. Những chú ý về số nguyên tố:
Những chú ý quan tâm về số nguyên tố
- Số nguyên tố nhỏ nhất và có 1 chữ số là số 2
- Số nguyên tố nhỏ nhất có 2 chữ số là số 11
- Số nguyên tố nhỏ nhất có 3 chữ số là số 101
- Số nguyên tố lớn nhất có 2 chữ số là số 97
- Số nguyên tố lớn nhất có 3 chữ số là 997

>> Xem thêm : Cách tính ước chung lớn nhất nhanh gọn .
2. Các đặc thù đặc trưng của số nguyên tố
Một số đặc thù cơ bản của số nguyên tốt để các em áp dung bài tập nhanh hơn :
Số 2 là số nguyên tố chẵn duy nhất và nhỏ nhất .
Số nguyên tố là vô hạn. Số lượng thành phần trong tập hơn số nguyên tố là không số lượng giới hạn .
Khi hai số nguyên tố nhân với nhau thì tích của chúng không hề là một số ít chính phương .
Ước tự nhiên nhỏ nhất khác 1 của một số ít tự nhiên được coi là số nguyên tố .
Ước bé nhất là một số dương khác 1 của một tập hợp số b bất kể là một số nguyên tố nếu không vượt quá căn bậc hai của b .
>> Xem thêm : Giá trị tuyệt đối đi suốt quy trình toán học. Các dạng bài tập và kiến thức và kỹ năng .
3. Một số định nghĩa khác về số nguyên tố
Hai số a và b là 2 số nguyên tố cùng nhau khi chúng có ước chung lớn nhất là 1 .
Ví dụ : Cho hai số là 7 và 8. Hỏi hai số đó có phải số nguyên tố cùng nhau hay không ?
Lời giải :
– Ta có : 5 = 1 x 5 ; 9 = 1 x 3 × 3
– Nhận thấy ước chung lớn nhất của 5 và 9 là 1. Như vậy hoàn toàn có thể Kết luận hai số 5 và 9 là hai số nguyên tố cùng nhau .
Tương tự có các ví dụ tiếp theo :
– 2 và 7 được gọi là hai số nguyên tố cùng nhau vì chúng có ước số chung lớn nhất là 1 .
– 3 và 5 có ước số chung lớn nhất là 1 nên chúng là 2 số nguyên tố cùng nhau .
– 11 và 28 cũng là hai số nguyên tố cùng nhau bởi chúng có ước số chung lớn nhất là 1 .
– Hai số 6 và 27 không phải là hai số nguyên tố cùng nhau do ước số chung lớn nhất của chúng là 3, khác 1 .
>> Xem thêm : Kiến thức tia phân giác một trong những kỹ năng và kiến thức hình học cơ bản .
4. Một số bài tập số nguyên tố
Ví dụ 1: Chứng minh rằng các số sau đây là hợp số:
a ) 27 + 311 + 513 + 717 + 1119
b ) 1 + 2123 + 23124 + 25125
Hướng dẫn giải:
a ) Ta có : 27 + 311 + 513 + 717 + 1119
Theo quy ước ta có :
27 có chữ số tận cùng là 8
311 có chữ số tận cùng là 7
513 luôn có chữ số tận cùng là 5
717 có chữ số tận cùng là 7
1119 luôn có chữ số tận cùng là 1
Ta có : 27 + 311 + 513 + 717 + 1119 có chữ số tận cùng là 8
Suy ra 27 + 311 + 513 + 717 + 1119 chia hết cho 2 .
Vậy, đây là hợp số .
b ) Ta có : 1 + 2123 + 23124 + 25125
2123 có chữ số tận cùng là 1
23124 có chữ số tận cùng là 1 ( các số có chữ số tận cùng là 3 khi nâng lên lũy thừa bậc 4 n ( n là số tự nhiên ) thì có chữ số tận cùng là 1. Số đã cho có số mũ là 124 = 4.31 )
25125 luôn có chữ số tận cùng là 5
Nên 1 + 2123 + 23124 + 25125 có chữ số tận cùng là 8
suy ra 1 + 2123 + 23124 + 25125 chia hết cho 2 .
vậy, đây là hợp số .
>> Xem thêm : Quy tắc dấu ngoặc bài tập kiến thức và kỹ năng cơ bản .
Ví dụ 2: Chứng minh rằng nếu ba số a, a+k, a+2k đều là các số nguyên tố lớn hơn 3, thì k chia hết cho 6
Hướng dẫn giải:
Do a, a + k, a + 2 k đều là nguyên tố lớn hơn 3 nên đều là số lẻ và không chia hết cho 3 .
• Vì a và a + k cùng lẻ nên a + k – a = k ⋮ 2. ( 1 )
• Vì a, a + k, a + 2 k đều không chia hết cho 3 nên khi chia cho 3 tối thiểu hai số có cùng số dư, khi đó :
+ Nếu a và a + k có cùng số dư, thì suy ra : ( a + k ) – a = k ⋮ 3
+ Nếu a + k và a + 2 k có cùng số dư, thì suy ra : ( a + 2 k ) – ( a + k ) = k ⋮ 3
+ Nếu a và a + 2 k có cùng số dư, thì suy ra :
( a + 2 k ) – a = 2 k 3 nhưng ( 2,3 ) = 1 nên k 3
Vậy, ta luôn có k chia hết cho 3 ( 2 )
Từ ( 1 ), ( 2 ) và do ( 2,3 ) = 1 ta suy ra k ⋮ 6, đpcm .
Nhận xét : Trong giải thuật trên, ta đã xu thế được rằng để chứng tỏ k ⋮ 6 thì cần chứng tỏ k ⋮ 2 và k ⋮ 3 và ở đó :
• Việc chứng tỏ k ⋮ 2 được nhìn nhận trải qua nhận định và đánh giá a, a + k, a + 2 k đều là nguyên tố lẻ hơn kém nhau k đơn vị chức năng .
• Việc chứng tỏ k ⋮ 3 được nhìn nhận trải qua đánh giá và nhận định “ ba số lẻ không chia hết cho 3 thì có tối thiểu hai số có cùng số dư ” và như vậy hiệu của hai số đó sẽ chia hết cho 3 .
Ví dụ 3: Ta biết rằng có 25 số nguyên tố nhỏ hơn 100. Tổng của 25 số nguyên tố đó là số chẵn hay lẻ?
Hướng dẫn giải:
Ta thấy trong 25 số nguyên tố có 1 số chẵn còn lại là 24 số lẻ. Tổng của 24 số lẻ là một số chẵn nên tổng của 25 số nguyên tố nhỏ hơn 100 là số chẵn .
Ví dụ 4: Tổng của ba số nguyên tố bằng 1012. Tìm số nhỏ nhất trong ba số nguyên tố đó.
Hướng dẫn giải:
Vì tổng của 3 số nguyên tố bằng 1012, nên trong 3 số nguyên tố đó sống sót một số nguyên tố chẵn. Mà số nguyên tố chẵn duy nhất là 2 và là số nguyên tố nhỏ nhất. Vậy số nguyên tố nhỏ nhất trong 3 số nguyên tố đó là 2
Chúc các bạn thành công xuất sắc !
Source: https://final-blade.com
Category : Kiến thức Internet