Bộ chuyển đổi và hướng dẫn nhị phân sang thập phân

Posted on by adminChuyên mục:Kiến thức Internet
converting binary to decimal

Cách chuyển đổi số nhị phân thành thập phân:

  • Bước 1: Viết trọng lượng liên quan dưới mỗi chữ số của số nhị phân. Trọng lượng là 2 bởi sức mạnh của vị trí của chữ số trong số đọc từ phải sang trái.
  • Bước 2: Bây giờ lưu ý trọng lượng mà giá trị nhị phân bằng 1.
  • Bước 3: Thêm tất cả các số thu được trong bước trước
  • Bước 4: Số từ bước cuối cùng sẽ là số thập phân tương đương với số nhị phân.

Chúng ta hãy xem xét một giá trị nhị phân 1101001 .
1. ) Bước tiên phong :
\begin{array}{|c|c|c|c|c|c|c|}
\hline
\text{Nhị phân } & \text{1} & \text{1} & \text{0} & \text{1} & \text{0} & \text{0} & \text{1} \\
\hline
\text{Trọng lượng liên quan } & \text{64} & \text{32} & \text{16} & \text{8} & \text{4} & \text{2} & \text{1} \\
\hline
\end{array}
\ begin { array } { | c | c | c | c | c | c | c | } \ hline \ text { Nhị phân } và \ text { 1 } và \ text { 1 } và \ text { 0 } và \ text { 1 } và \ text { 0 } và \ text { 0 } và \ text { 1 } \ \ \ hline \ text { Trọng lượng tương quan } và \ text { 64 } và \ text { 32 } và \ text { 16 } và \ text { 8 } và \ text { 4 } và \ text { 2 } và \ text { 1 } \ \ \ hline \ end { array }

2.) Bước thứ hai: Trọng lượng mà các chữ số nhị phân là 1.

\begin{array}{|c|c|c|c|c|c|c|}
\hline
\text{64} & \text{32} & \text{8} & \text{1} \\
\hline
\end{array}
\ begin { array } { | c | c | c | c | c | c | c | } \ hline \ text { 64 } và \ text { 32 } và \ text { 8 } và \ text { 1 } \ \ \ hline \ end { array }3. ) Bước thứ ba : Thêm toàn bộ các trọng số
USD USD 105 = 64 + 32 + 8 + 1 $ $
4. ) Bước ở đầu cuối : Tương đương thập phân của nhị phân là : : 105

Cách chuyển đổi số thập phân thành nhị phân:

Thực hiện theo các bước này, bạn hoàn toàn có thể quy đổi bất kể số thập phân nào thành mạng lưới hệ thống nhị phân :

  • Bước 1: Chia số thập phân cho 2 và ghi ra phần còn lại và gán giá trị r1 = phần còn lại, gán tương tự giá trị q1 = thương số thu được trong phân chia này.
  • Bước 2: Bây giờ chia q1 với 2 và lưu ý phần còn lại. Chỉ định giá trị của phần còn lại cho R2 và giá trị của thương số cho Q1.
  • Bước 3: Tiếp tục trình tự cho đến tại một số điểm trong một bộ phận, bạn nhận được giá trị của thương số (QN) bằng 0.
  • Bước 4: Bạn có thể viết số nhị phân như: $$ R(n) R(n-1). .. .. .. .. .. .. .. .. .. .. R3 R2 R1 $$

Ví dụ: Chúng ta hãy xem xét số thập phân 179.
\begin{array}{|c|c|c|c|c|c|c|}
\hline
\text{} & \text{ ÷ 2} & \text{Q} & \text{R} \\
\hline
\text{R1} & \text{179 / 2 = (89 × 2) + 1 } & \text{89} & \text{1} \\
\text{R2} & \text{89 / 2 = (44 × 2) + 1 } & \text{44} & \text{1} \\
\text{R3} & \text{ 44 / 2 = (22 × 2) + 0 } & \text{44} & \text{0} \\
\text{R4} & \text{ 22 / 2 = (11 × 2) + 0 } & \text{11} & \text{0} \\
\text{R5} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{5} & \text{1} \\
\text{R6} & \text{ 11 / 2 = (5 × 2) + 1 } & \text{2} & \text{1} \\
\text{R7} & \text{ 2 / 2 = (1 × 2) + 0 } & \text{1} & \text{0} \\
\text{R8} & \text{ 1 / 2 = (0 × 2) + 1 } & \text{0} & \text{1} \\
\hline
\end{array}
Bây giờ bạn có thể viết ra số nhị phân từ phần còn lại, bắt đầu bằng R8:
\begin{array}{|c|c|c|c|c|c|c|}
\hline
\text{R8} & \text{R7} & \text{R6} & \text{R5} & \text{R4} & \text{R3} & \text{R2} & \text{R1} \\
\hline
\text{1} & \text{0} & \text{1} & \text{1} & \text{0} & \text{0} & \text{1} & \text{1} \\
\hline
\end{array}
Ví dụ : Chúng ta hãy xem xét số thập phân 179. \ begin { array } { | c | c | c | c | c | c | c | } \ hline \ text { } và \ text { ÷ 2 } và \ text { Q. } và \ text { R } \ \ \ hline \ text { R1 } và \ text { 179 / 2 = ( 89 × 2 ) + 1 } và \ text { 89 } và \ text { 1 } \ \ \ text { R2 } và \ text { 89 / 2 = ( 44 × 2 ) + 1 } và \ text { 44 } và \ text { 1 } \ \ \ text { R3 } và \ text { 44 / 2 = ( 22 × 2 ) + 0 } và \ text { 44 } và \ text { 0 } \ \ \ text { R4 } và \ text { 22 / 2 = ( 11 × 2 ) + 0 } và \ text { 11 } và \ text { 0 } \ \ \ text { R5 } và \ text { 11 / 2 = ( 5 × 2 ) + 1 } và \ text { 5 } và \ text { 1 } \ \ \ text { R6 } và \ text { 11 / 2 = ( 5 × 2 ) + 1 } và \ text { 2 } và \ text { 1 } \ \ \ text { R7 } và \ text { 2 / 2 = ( 1 × 2 ) + 0 } và \ text { 1 } và \ text { 0 } \ \ \ text { R8 } và \ text { 1 / 2 = ( 0 × 2 ) + 1 } và \ text { 0 } và \ text { 1 } \ \ \ hline \ end { array } Bây giờ bạn hoàn toàn có thể viết ra số nhị phân từ phần còn lại, khởi đầu bằng R8 : \ begin { array } { | c | c | c | c | c | c | c | } \ hline \ text { R8 } và \ text { R7 } và \ text { R6 } và \ text { R5 } và \ text { R4 } và \ text { R3 } và \ text { R2 } và \ text { R1 } \ \ \ hline \ text { 1 } và \ text { 0 } và \ text { 1 } và \ text { 1 } và \ text { 0 } và \ text { 0 } và \ text { 1 } và \ text { 1 } \ \ \ hline \ end { array }

(179) SỐ THẬP PHÂN = (10110011) Nhị phân

Làm thế nào để bạn chuyển đổi các chữ số sau điểm thập phân giữa hệ thống nhị phân và số thập phân?

Cho đến nay, chúng tôi đã học được cách chuyển đổi số nguyên giữa nhị phân và thập phân. Làm thế nào về những con số với các vị trí thập phân? Quy trình tương tự như các bước trên. Đầu tiên, chia số vào phần của nó trước và sau vị trí thập phân. Hãy xem xét số thập phân 1932.1875:

Nó gồm có một số ít nguyên Phần 1932 và phân số 0,1875. Đối với số nguyên Phần 1932, hãy sử dụng các bước từ trên cao. Kết quả tương tự nhị phân là : 11110001100 .
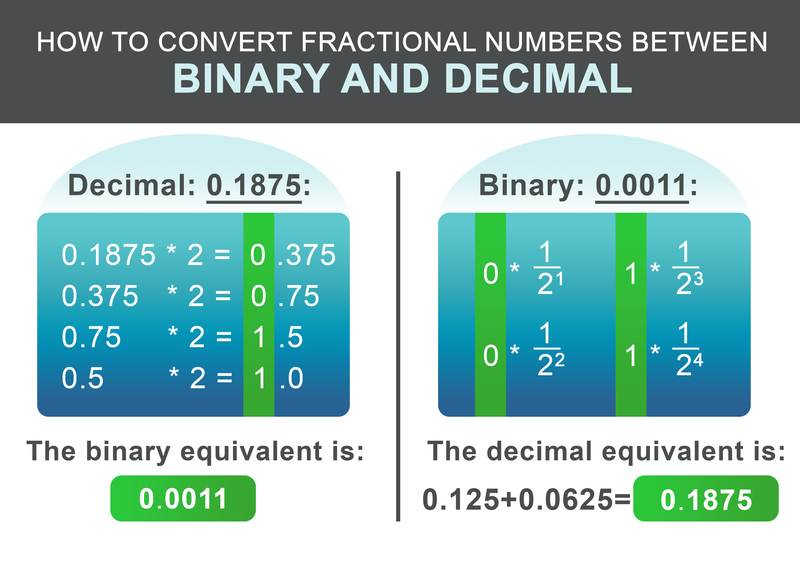
Phần phân số 0.1875 hoàn toàn có thể được quy đổi theo lược đồ sau. Nhân đệ tử nhân phần phe phái với hai. Nếu hiệu quả vượt quá 1, hãy ghi 1 và sau đó trừ 1 từ số tác dụng. Nếu hiệu quả nhỏ hơn một lần ghi 0. Tiếp theo, hãy liên tục nhân với hai. Nếu không, hãy viết ra 0 .
converting binary to decimal
Đối với ví dụ của chúng tôi 0.1875, số nhị phân hiệu quả là : 0,0011 trong bước sau cuối, thêm các phần số nguyên và phân đoạn :
USD $ 11110001100.0011 $ $
Để quy đổi phe nhị phân trở lại, quy trình tiến độ thao tác thậm chí còn còn đơn thuần hơn. Thêm $ 1/2 ^ i USD cho mỗi chữ số sau dấu chấm vào hiệu quả, theo đó tôi là vị trí của chữ số sau từ trái sang phải, mở màn từ 1 .
USD USD 0 * \ frac { 1 } { 2 ^ 1 } + 0 * \ frac { 1 } { 2 ^ 2 } + 1 * \ frac { 1 } { 2 ^ 3 } + 1 * \ frac { 1 } { 2 ^ 4 } = 0.1875 $ $

Hệ thống nhị phân và các ứng dụng của nó

Một mạng lưới hệ thống số là một tập hợp các tích hợp các hình tượng khác nhau, với mỗi hình tượng có khối lượng đơn cử. Các đặc thù chính của một mạng lưới hệ thống số là radix hoặc cơ sở xác lập tổng số ký hiệu được sử dụng trong một mạng lưới hệ thống số đơn cử. Ví dụ, radix của mạng lưới hệ thống nhị phân là 2 và radix của mạng lưới hệ thống số thập phân là 10 .

Không gian chữ số của hệ thống nhị phân

Trong hệ thống nhị phân, chúng ta có hai chữ số riêng biệt: 0 và 1. Trong máy tính, chúng ta có các thiết bị như flip-flops có thể lưu trữ bất kỳ cấp độ nào trong hai cấp theo tín hiệu điều khiển. Mức cao hơn được gán giá trị 1 và mức thấp hơn được gán giá trị 0, do đó tạo thành một hệ thống nhị phân.

Tầm quan trọng của hệ thống nhị phân trong điện toán:

Một máy tính sử dụng hàng tỷ và hàng tỷ bóng bán dẫn hoạt động giải trí kỹ thuật số. Thuật ngữ kỹ thuật số tương quan đến các mức logic rời rạc. Mức logic là các cấp tiềm năng khác nhau như 5V, 0V, 10V và nhiều Lever khác .
Bất kỳ máy tính nào hoạt động giải trí bằng logic nhị phân, vì thế nếu tất cả chúng ta muốn đại diện thay mặt cho máy tính, tất cả chúng ta phải viết các số có radix bằng 2. Hai ký hiệu trong mạng lưới hệ thống số này tựa như như hai mức logic rời rạc. Để thuận tiện, chúng tôi coi hai hình tượng này là 0 và 1, nhưng so với máy tính 0 và 1 là các mức điện áp khác nhau. Nói chung, 0 được xem xét cho mức điện áp thấp hơn và 1 được xem xét cho mức điện áp cao hơn .

Tất cả những gì tất cả chúng ta thấy trên màn hình hiển thị của máy tính hoặc cung ứng nguồn vào trải qua chuột hoặc bàn phím đều là 0 và 1, sự độc lạ duy nhất là sự sắp xếp tuần tự của chúng. Vì vậy, nếu tất cả chúng ta muốn triển khai xong việc làm của mình từ máy tính, tất cả chúng ta phải biết phương pháp hoạt động giải trí của nhị phân và mối quan hệ của nhị phân với số thập phân để quy đổi các giá trị từ miền nhị phân thành miền đã biết của tất cả chúng ta .

admin