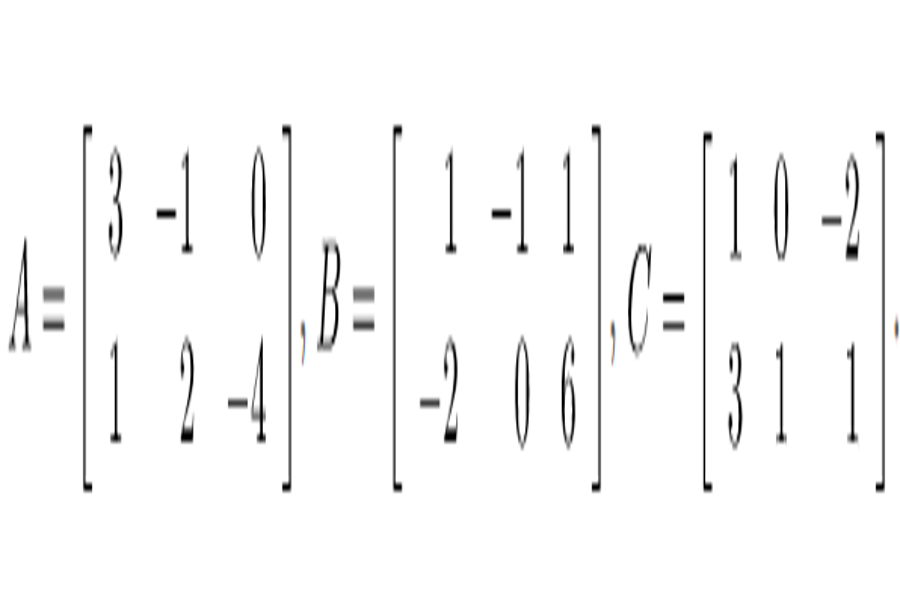
Tóm Tắt
1. Ma trận là gì ?
Hầu hết một dãy số hình chữ nhật được gọi là ma trận, và các số được gọi là các phần tử ma trận. Ma trận thường được ký hiệu bằng chữ cái in hoa: A,B,C
-
Ma trận cỡ m x n là 1 bảng số hình chữ nhật gồm m hàng, n cột
-
Kí hiệu ma trận : A = (aij) m x n
- Ví dụ dưới đây là một ma trận :
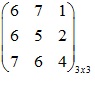
Ma trận có nhiều hình dạng khác nhau tuỳ thuộc vào số hàng và cột. Ví dụ ma trận trên có 3 hàng và 3 cột. Thường thì ma trận với m hàng và n cột thường được gọi là ma trận m x n. Với ma trận có kích thước 1 x n được gọi là ma trận hàng, ma trận có kích thước m x 1 được gọi là ma trận cột. Ma trận cỡ n x n được gọi là ma trận vuông.
Phần tử của ma trận được xác định bởi hàng và cột của nó. Các hàng được đánh số từ trên xuống dưới, và các cột được đánh số từ trái qua phải. Do đó, phần tử (i,j) của ma trận là phần tử hàng i, cột j.
Với ma trận A là ma trận 3 × 4 có aij. Thì ma trận A được bộc lộ như sau :

Tóm lại:
- Nếu ma trận cỡ m x n, thì nó có m hàng và n cột.
- Phần tử ma trận aij nghĩa là phần tử nằm ở hàng i cột j.
2. Các ma trận đặc biệt quan trọng
a. Ma trận 0: các phần tử đều bằng 0
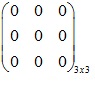
b. Ma trận đường chéo : Ma trận vuông mà các thành phần ngoài đường chéo chính bằng 0

c. Ma trận đơn vị chức năng : Ma trận có các thành phần đường chéo = 1
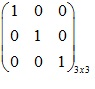
d. Ma trận tam giác trên : Ma trận vuông mà các thành phần nằm dưới đường chéo chính = 0

e. Ma trận chuyển vị của A :
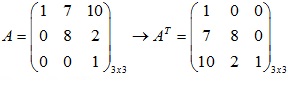
f. Các đặc thù của ma trận
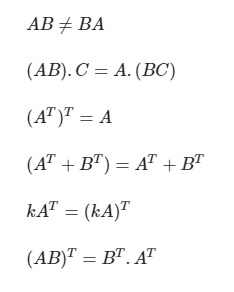
g. Ma trận bậc thang
- Nếu các hàng = 0 thì phải ở dưới cùng
- Nếu các hàng ≠ 0 thì thành phần tiên phong của hàng dưới phải lệch sang phải thành phần ≠ 0 tiên phong hàng trên

Xem thêm cách tính hạng của ma trận : Hạng của ma trận – bài tập và giải thuật chi tiết cụ thể
4. Phép cộng 2 ma trận
Nếu A và B là 2 ma trận cùng cỡ, thì ma trận A + B được tính bằng cách cộng các thành phần cùng vị trí .
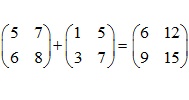
Lưu ý: Không cộng 2 ma trận khác kích cỡ.
Tính chất:
- Với A, B, C là ma trận bất kỳ cùng cỡ thì: A+B = B+A ; A+(B+C) = (A+B)+C
- Ma trận nào cộng với ma trận không cũng bằng chính nó: 0+X=X
- Phép trừ ma trận: A-B được xác định bởi: A-B=A+(-B)
Ví dụ 1: Tính -A, A-B và A+B-C các ma trận sau:
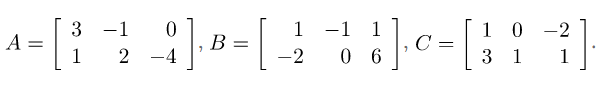

Ví dụ 2: Tìm ma trận X sau:
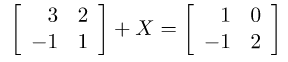
Giải
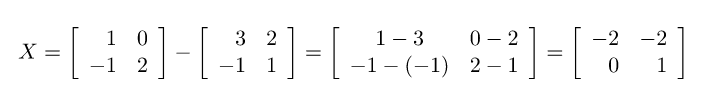
5. Phép nhân 2 ma trận
5.1 Nhân ma trận với 1 số bất kỳ
Nếu A là một ma trận bất kể và k là một số ít bất kể thì ma trận kA được tính bằng cách nhân từng thành phần của ma trận A với k
Ví dụ nhân ma trận với 1 số:
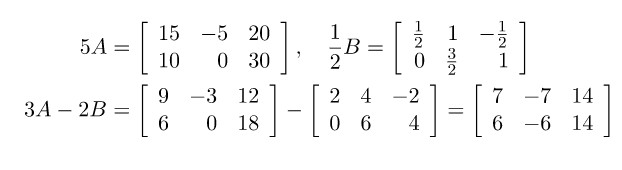
Lưu ý:
Nếu A là một ma trận bất kể, thì ma trận kA có kích cỡ giống A và : 0A = 0 ; k0 = 0
5.2 Cách nhân 2 ma trận
Muốn nhân ma trận A với ma trận B thì phải có điều kiện kèm theo :
- số cột ma trận A bằng số hàng ma trận B
Lấy phần tử đứng ở hàng i cột j trong ma trận A, ta lấy lần lượt từng phần tử đứng ở hàng i trong ma trận A nhân với
từng phần tử tương ứng đứng ở cột j trong ma trận B rồi cộng lại.
Ví dụ :
1.1 + 1.3 = 4 1.2 + 1.4 = 6 1.3 + 1.4 = 7
3.1 + 7.3 = 24 3.2 + 7.4 = 34 3.3 + 7.4 = 37
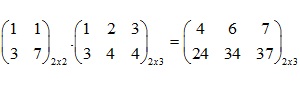
6. Định lý
Với A, B và C là ma trận cỡ m x n bất kỳ. Với k và p là số thực bất kỳ thì có định lý của ma trận:
- A+B=B+A
- A+(B+C) = (A+B)+C
- Ma trận 0 cỡ m x n thì 0 + A = A
- Với mỗi A là ma trận bất kỳ cỡ m x n, -A thì A +(-A)=0
- k(A+B)=kA+kB
- (k+p)A=kA+pA
- (kp)A=k(pA)
- 1A=A
Các dạng bài tập ma trận và cách giải
1.Tìm ma trận A thoả mãn:
a /
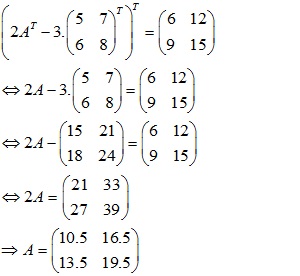
b /
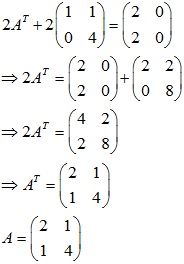
2. Bài tập nhân 2 ma trận toán cao cấp
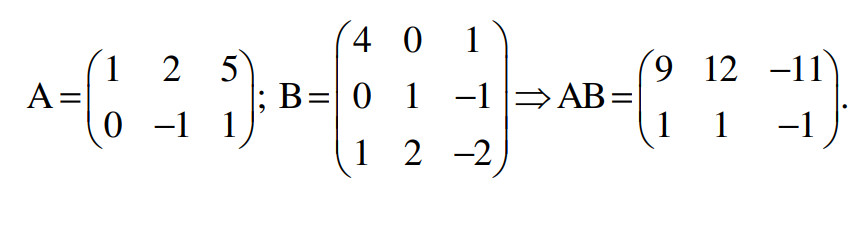
Bài viết tương quan : Độc lập tuyến tính và Phụ thuộc tuyến tính – Bài tập và lời giải
3. Bài tập ma trận bậc thang có lời giải
Ví dụ : Đưa ma trận sau về ma trận bậc thang :
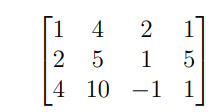
Hướng dẫn giải

Như vậy ta đã hoàn thành đưa ma trận về dạng ma trận bậc thang
Xem thêm : Ma trận nghịch đảo
Tải file bài tập về ma trận và lý thuyết ma trận
Hi vọng qua bài viết trên các bạn đã nắm vững kiến thức cơ bản và biết cách giải ma trận theo yêu cầu bài toán môn đại số và hình giải tích. Cảm ơn các bạn đã tham khảo tài liệu trên ttnguyen.net
Source: https://final-blade.com
Category : Kiến thức Internet