Giai thừa – Là gì Wiki

Hai công thức dưới đây là do Gauss chứng tỏ :

$\backslash Gamma\backslash left(\backslash frac\{1\}\{2\}+n\backslash right)\; =\; \{(2n)!\; \backslash over\; 4^n\; n!\}\; \backslash sqrt\{\backslash pi\}\; =\; \backslash frac\{(2n-1)!!\}\{2^n\}\backslash ,\; \backslash sqrt\{\backslash pi\}\; =\; \backslash sqrt\{\backslash pi\}\; \backslash cdot\; \backslash left[\; \{n-\backslash frac\{1\}\{2\}\backslash choose\; n\}\; n!\; \backslash right]$

$\backslash Gamma\backslash left(\backslash frac\{1\}\{2\}-n\backslash right)\; =\; \{(-4)^n\; n!\; \backslash over\; (2n)!\}\; \backslash sqrt\{\backslash pi\}\; =\; \backslash frac\{(-2)^n\}\{(2n-1)!!\}\backslash ,\; \backslash sqrt\{\backslash pi\}\; =\; \backslash sqrt\{\backslash pi\}\; /\; \backslash left[\; \{-\backslash frac\{1\}\{2\}\; \backslash choose\; n\}\; n!\; \backslash right]$

Giai thừa với số thực

Giai thừa với số thực .Theo công thức tương ứng giữa giai thừa với công thức Gamma, những nhà toán học đã đề ra công thức Pi có dạng sau :

$z!\; =\; \backslash Pi(z)\; =\; \backslash Gamma(z+1)\; \backslash ,.$

Như vậy :

$(-0,5)!\; =\; \backslash Pi\; \backslash left(-\backslash frac\{1\}\{2\}\; \backslash right)\; =\; \backslash Gamma\; \backslash left(\backslash frac\{1\}\{2\}\; \backslash right)\; \backslash ,.$

$(n\; –\; 0,5)!\; =\; \backslash Pi\; \backslash left(n\; –\; \backslash frac\{1\}\{2\}\; \backslash right)\; =\; \backslash Gamma\; \backslash left(n\; +\; \backslash frac\{1\}\{2\}\; \backslash right)\; \backslash ,.$

$(-n\; –\; 0,5)!\; =\; \backslash Pi\; \backslash left(-n\; –\; \backslash frac\{1\}\{2\}\; \backslash right)\; =\; \backslash Gamma\; \backslash left(-n\; +\; \backslash frac\{1\}\{2\}\; \backslash right)\; \backslash ,.$

Ví dụ :

• $\backslash Gamma\backslash left\; (4.5\; \backslash right)\; =\; 3.5!\; =\; \backslash Pi\backslash left\; (3.5\backslash right)\; =\; \{1\backslash over\; 2\}\backslash cdot\{3\backslash over\; 2\}\backslash cdot\{5\backslash over\; 2\}\backslash cdot\{7\backslash over\; 2\}\; \backslash sqrt\{\backslash pi\}\; =\; \{8!\; \backslash over\; 4^4\; 4!\}\; \backslash sqrt\{\backslash pi\}\; =\; \{105\; \backslash over\; 16\}\; \backslash sqrt\{\backslash pi\}\; \backslash approx\; 11.63.$
• $\backslash Gamma\backslash left\; (-2.5\; \backslash right)\; =\; (-3.5)!\; =\; \backslash Pi\backslash left\; (-3.5\backslash right)\; =\; \{2\backslash over\; -1\}\backslash cdot\{2\backslash over\; -3\}\backslash cdot\{2\backslash over\; -5\}\; \backslash sqrt\{\backslash pi\}\; =\; \{(-4)^3\; 3!\; \backslash over\; 6!\}\; \backslash sqrt\{\backslash pi\}\; =\; -\{8\; \backslash over\; 15\}\; \backslash sqrt\{\backslash pi\}\; \backslash approx\; -0.9453.$

Giai thừa với số phức

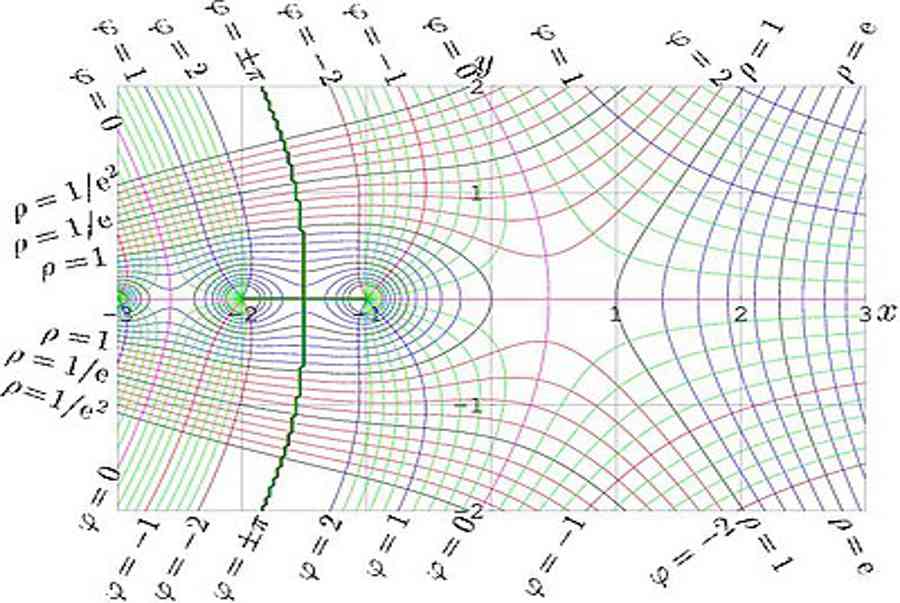
Đồ thị đường đồng mức của hàm giai thừa biến phức .Công thức chính để tính giai thừa trong trường hợp này là ước đạt Laurent :

$\backslash Gamma(z)\; =\; \backslash sum\_\{k=0\}^\backslash infty\backslash frac\{\backslash Gamma^\{(k)\}(1)\}\{k!\}z^\{k-1\}\backslash ,,$

với | z | < 1. Khai triển ra ta có bảng những thông số như sau :

$n$	$g\_n$	approximation
0	$1$	$1$
1	$-\backslash gamma$	$–\; 0.5772156649$
2	$\backslash frac\{\backslash pi^2\}\{12\}+\backslash frac\{\backslash gamma^2\}\{2\}$	$0.9890559955$
3	$-\backslash frac\{\backslash zeta(3)\}\{3\}-\backslash frac\{\backslash pi^2\backslash gamma\}\{12\}-\backslash frac\{\backslash gamma^3\}\{6\}$	$-0.9074790760$

Ở đây

$\backslash gamma$

là hằng số Euler – Mascheroni còn

$\backslash zeta$

là hàm zeta Riemann.

• .
• Đồ thị hàm Z = Re ( z ! ) .
• Đồ thị hàm Z = Im ( z ! ) .

Các khái niệm tựa như

Giai thừa nguyên tố (primorial)

Bài chi tiết cụ thể : Giai thừa nguyên tố

Giai thừa nguyên tố (ký hiệu n#) với n>1 là tích của tất cả các số nguyên tố nhỏ hơn hoặc bằng n. Chẳng hạn, 7# = 210 là tích các số nguyên tố (2·3·5·7). Tên này đặt theo Harvey Dubner và là từ ghép của prime và factorial. Các giai thừa nguyên tố đầu tiên là:

2, 6, 30, 210, 2310, 30030, 510510, 9699690, 223092870, 6469693230, 200560490130, 7420738134810, 304250263527210, 13082761331670030, 614889782588491410 (theo OEIS).

Giai thừa kép

Có thể coi n! là tích n phần tử đầu của cấp số cộng với phần tử đầu bằng 1 và công sai bằng 1. Mở rộng với công sai bằng 2 ta có:

Giai thừa kép là tích n phần tử đầu của cấp số cộng với phần tử đầu 1 và công sai là 2.

$$

n!!=
 \left\{
  \begin{matrix}
   1,\qquad\quad\ &&\mbox{khi }n<=1;
  \\
   n(n-2)!!&&\mbox{khi }n\ge2.\qquad\qquad
  \end{matrix}
 \right.

Ví dụ :

8!! = 2 · 4 · 6 · 8 = 384

9!! = 1 · 3 · 5 · 7 · 9 = 945.

Dãy những giai thừa kép tiên phong là :

n	0	1	2	3	4	5	6	7	8	9	10
n!!	1	1	2	3	8	15	48	105	384	945	3840

Định nghĩa trên hoàn toàn có thể lan rộng ra cho những số nguyên âm như sau :

$(n-2)!!=\backslash frac\{n!!\}\{n\}$

Các giai thừa kép nguyên âm lẻ đầu tiên với n= -1, -3, -5, -7,...là

1, -1, 1/3, -1/15...

Các giai thừa kép của số nguyên âm chẵn là không xác lập .Một vài đẳng thức với giai thừa kép :

$n!=n!!(n-1)!!\; \backslash ,$

$(2n)!!=2^nn!\; \backslash ,$

$(2n+1)!!=\{(2n+1)!\backslash over(2n)!!\}=\{(2n+1)!\backslash over2^nn!\}$

Cũng nên phân biệt n!! với (n!)!.

Giai thừa bội

Ta có thể tiếp tục mở rộng với các giai thừa bội ba (n!!!),bội bốn (n!!!!)....

Tổng quát, giai thừa bội k ký hiệu là n!(k), được định nghĩa đệ quy như sau

$$

 n!^{(k)}=
 \left\{
  \begin{matrix}
   1,\qquad\qquad\ &&\mbox{khi }0\le n

Siêu giai thừa(superfactorial)

Neil Sloane và Simon Plouffe đã định nghĩa siêu giai thừa (năm 1995) là tích của n giai thừa đầu tiên. Chẳng hạn, siêu giai thừa của 4 là

$\backslash mathrm\{sf\}(4)=1!\; \backslash times\; 2!\; \backslash times\; 3!\; \backslash times\; 4!=288\; \backslash ,$

Tổng quát

$$

 \mathrm{sf}(n)
 =\prod_{k=1}^n k! =\prod_{k=1}^n k^{n-k+1}
 =1^n\cdot2^{n-1}\cdot3^{n-2}\cdots(n-1)^2\cdot n^1.

Các siêu giai thừa đầu tiên bắt đầu từ n = 0) là

Vào năm 2000, tư tưởng này được Henry Bottomley mở rộng thành siêu giả giai thừa (superduperfactorial) là tích của n siêu giai thừa đầu tiên. Những giá trị đầu tiên của chúng là (bắt đầu từ n = 0):

1, 1, 2, 24, 6912, 238878720, 5944066965504000,...

và tiếp tục đệ quy với siêu giai thừa bội (multiple-level factorial) trong đó siêu giai thừa bội cấp m của n là tích của n siêu giai thừa bội cấp(m − 1), nghĩa là

$\backslash mathrm\{mf\}(n,m)\; =\; \backslash mathrm\{mf\}(n-1,m)\backslash mathrm\{mf\}(n,m-1)$

=\prod_{k=1}^n k^{n-k+m-1 \choose n-k} 

trong đó

$\backslash mathrm\{mf\}(n,0)=n$

for

$n>0$

and

$\backslash mathrm\{mf\}(0,m)=1$

.

Giai thừa trên

$x^\{\backslash overline\{n\}\}=x(x+1)(x+2)\backslash cdots(x+n-1)=\backslash frac\{(x+n-1)!\}\{(x-1)!\}$

Tham khảo

Liên kết ngoài

Thể loại : Lý thuyết số Thể loại : Toán học tổng hợp