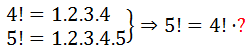
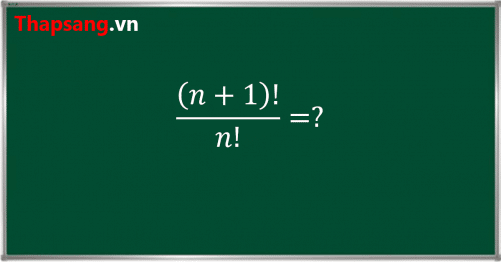 Tuy nhiên, trong SGK Đại số và Giải tích lớp 11, khái niệm Giai thừa chỉ Open ở dạng “ đề cập ” mà không được ra mắt một cách rất đầy đủ và hầu hết không có bài tập củng cố khái niệm này. Bài viết này mình san sẻ với những bạn một số ít kinh nghiệm tay nghề dạy và học, đặc biệt quan trọng là “ khẩu quyết ” khi vận dụng nó trong quy trình giải toán. Hy vọng bài viết có ích cho bạn .
Tuy nhiên, trong SGK Đại số và Giải tích lớp 11, khái niệm Giai thừa chỉ Open ở dạng “ đề cập ” mà không được ra mắt một cách rất đầy đủ và hầu hết không có bài tập củng cố khái niệm này. Bài viết này mình san sẻ với những bạn một số ít kinh nghiệm tay nghề dạy và học, đặc biệt quan trọng là “ khẩu quyết ” khi vận dụng nó trong quy trình giải toán. Hy vọng bài viết có ích cho bạn .Trước tiên, tất cả chúng ta cần hiểu “ Giai thừa ” là gì ?
Tóm Tắt
1. Định nghĩa
![]() là số tự nhiên dương. Tích của số tự nhiên liên tiếp từ 1 đến được gọi là n – giai thừa. Kí hiệu là
là số tự nhiên dương. Tích của số tự nhiên liên tiếp từ 1 đến được gọi là n – giai thừa. Kí hiệu là ![]()
Cholà số tự nhiên dương. Tích củasố tự nhiên liên tiếp từ 1 đếnđược gọi là n – giai thừa. Kí hiệu là
Như vậy, kí hiệu là một số ít nguyên dương được tính bởi công thức
hoặc
Ví dụ
Tích của 1 số từ 1 đến 1
Tích của 2 số liên tục, từ 1 đến 2
Tích của 3 số liên tục, từ 1 đến 3
Tích của 4 số liên tục, từ 1 đến 4
Tích của 5 số liên tục, từ 1 đến 5
chỉ được định nghĩa với là một số tự nhiên lớn hơn không. Về sau để tiện sử dụng và phù hợp với một số công thức tính toán, người ta “mở rộng” khái niệm Giai thừa cho trường hợp bằng 0 và định nghĩa – hay qui ước:
. Bạn có thể Google hoặc xem trên Theo định nghĩa trên, khái niệmchỉ được định nghĩa vớilà một số ít tự nhiên lớn hơn không. Về sau để tiện sử dụng và tương thích với 1 số ít công thức thống kê giám sát, người ta “ lan rộng ra ” khái niệm Giai thừa cho trường hợpbằng 0 và định nghĩa – hay quy ước :. Bạn hoàn toàn có thể Google hoặc xem trên Wikipedia để tìm hiểu và khám phá thêm về quy ước này !
Quy ước:
Điều kiện xác định
Với quy ước trên, từ giờ trở đi tất cả chúng ta cần nhớ
chỉ có nghĩa khihay
Kí hiệuchỉ có nghĩa khihayTiếp theo, tất cả chúng ta cùng khám phá xem Giai thừa có đặc thù gì đặc biệt quan trọng .
2. Tính chất giai thừa
Hãy quay lại ví dụ ở trên, quan sát các giai thừa khi viết chúng ở dạng tích các số tự nhiên liên tiếp và cố gắng tìm ra một mối liên hệ nào đó giữa các giai thừa lớn so với các giai thừa bé hơn. Chẳng hạn, giữa
và
hay giữa và
?
Bạn có thấy mối quan hệ gì không ?
Đó là, có thể viết
,
và
, tương tự bạn có thể suy ra
,… và tổng quát ta có:
hay
với
hayvớiĐây chính là đặc thù đặc trưng của Giai thừa : Một giai thừa lớn luôn hoàn toàn có thể màn biểu diễn qua một giai thừa bé hơn. Chúng ta hoàn toàn có thể phát biểu đặc thù này dưới dạng “ khẩu quyết ” cho dễ nhớ là : “ Giai thừa lớn chứa giai thừa bé ”. Bây giờ hãy xem khẩu quyết này lợi hại thế nào 😀
3. Ví dụ
Ví dụ 1: Rút gọn biểu thức
Không dùng máy tính, rút gọn biểu thức sau :
Phân tích
* Nhận xét, biểu thức đã cho gồm những tỉ số mà tử và mẫu đều là những giai thừa, do đó ta hoàn toàn có thể vận dụng định nghĩa để viết từng giai thừa thành tích những thừa số rồi rút gọn. Nhưng rõ ràng, làm như vậy sẽ khiến biểu thức của ta rất cồng kềnh vì có rất nhiều thừa số .
* Để ý rằng, ở mỗi tỉ số đều chứa những giai thừa lớn và giai thừa nhỏ. Như vậy, ta có thể biểu diễn giai thừa lớn theo giai thừa nhỏ hơn rồi rút gọn. Chẳng hạn
, do đó
* Tương tự như vậy, cho các giai thừa còn lại:
và
. Từ đó, ta sẽ rút gọn được biểu thức một cách dễ dàng hơn.
Lời giải
Ta có
Do đó :
Bình luận: Qua ví dụ này ta rút được kinh nghiệm sau, khi rút gọn một tỉ sổ mà tử và mẫu đều chứa các giai thừa thì ta có thể làm như sau:
– Cách thứ nhất là: Áp dụng định nghĩa Giai thừa, viết các giai thừa dưới dạng tích số từ 1 đến rồi rút gọn các thừa số chung.
– Cách thứ hai là : Quan sát xem giai thừa nào lớn hơn, rồi giữ nguyên giai thừa bé và trình diễn giai thừa lớn theo giai thừa bé để rút gọn .
Theo bạn thì tất cả chúng ta nên dùng cách nào ? Trong ví dụ trên ta sử dụng phối hợp cả 2 cách, tiên phong tất cả chúng ta dùng cách thứ hai để triệt tiêu những “ giai thừa chung ”, sau đó dùng cách thứ nhất để rút gọn những thừa số chung. Qua đó, ta thấy rằng, sử dụng cách thứ hai để triệt tiêu những “ giai thừa chung ” là rất nhanh gọn và hiệu suất cao ! Vậy nhớ nhé, hãy luôn quan sát xem giai thừa nào lớn hơn, rồi trình diễn nó theo giai thừa bé hơn. Đó chính là “ khẩu quyết ” mà tất cả chúng ta đang khám phá .Ví dụ 2: Rút gọn biểu thức
Rút gọn biểu thức sau :
Phân tích
* Nhận xét, không giống như ví dụ trước, ở ví dụ này Open giai thừa có chứa biến. Tuy nhiên, điều đó không quan trọng ! Điều quan trọng là phải nhìn ra giai thừa nào là giai thừa lớn và giai thừa nào là giai thừa bé hơn .
* Dễ thấy,
lớn hơn
một đơn vị, do đó
và
Lời giải
Bình luận:
– Nếu dùng Cách thứ nhất, tức là vận dụng định nghĩa giai thừa để viết những giai thừa chứa biến kia thành tích những thừa số từ 1 đến, thì giải thuật của bạn sẽ như thế nào ? Cứ thử đi, thử rồi bạn sẽ càng thấy “ khẩu quyết ” của tất cả chúng ta thật lợi hại 😀
– Nhớ nhé, điều quan trọng là phải nhìn ra “ Giai thừa nào lớn hơn giai thừa nào ” sau đó thì cứ khẩu quyết “ Giai thừa lớn chứa giai thừa bé ” mà vận dụng, dù rằng giai thừa có chứa biến gì đi chăng nữa .Ví dụ 3: Giải phương trình chứa ẩn trong giai thừa
Giải phương trình
Phân tích
* Chà, một phương trình lạ mắt, một phương trình ẩn
mà lại nằm trong giai thừa! Lạ quá, từ xưa đến giờ chúng ta chỉ giải các phương trình mà ẩn nằm trong đa thức, căn thức và gần đây nhất là trong đối số của hàm lượng giác thôi. Giờ ẩn lại nằm trong giai thừa! Vậy làm thế nào để tìm đây?1
* Bình tĩnh một chút ít, hãy nhớ lại xem những “ sư phụ ” 😀 thường bảo tất cả chúng ta làm gì khi gặp những “ phương trình mới mẻ và lạ mắt ”, những phương trình mà tất cả chúng ta chưa biết giải ? À, “ khẩu quyết ” 2 hay dùng khi đó là “ đưa nó về phương trình đã biết giải ” hay “ quy lạ về quen ”. Vậy hãy triển khai vài phép rút gọn vế trái xem phương trình hoàn toàn có thể trở thành như thế nào ?
* Dễ thấy rằng
là bé nhất nên ta sẽ biểu diễn các giai thừa còn lại theo
, khi đó vế trái của phương trình đã cho trở thành
Tốt rồi, giai thừa đã bị “ biến mất ”, vế trái trở thành 1 biểu thức quen thuộc với tử là bậc nhất còn mẫu là bậc hai với ẩn, trong khi vế phải là hằng số. Do đó, nhân chéo, chuyển vế và rút gọn thì phương trình đã cho trở thành một phương trình bậc hai quen thuộc .
* Trước khi thực hiện lời giải, chú ý rằng chúng ta đang giải phương trình có chứa ẩn trong giai thừa nên phải có điều kiện cho ẩn. Dễ thấy, điều kiện ở đây là
.
Lời giải
* Điều kiện :
* Ta có :* Do đó, phương trình đã cho tương tự với phương trình
™,
™
* Kết luận: Phương trình đã cho có hai nghiệm
Bình luận:
– Ở ví dụ này, một lần nữa tất cả chúng ta được tận mắt chứng kiến sự “ lợi hại ” của khẩu quyết “ Giai thừa lớn chứa giai thừa bé ”. Nó giúp tất cả chúng ta xử lý bài toán thật “ ngon lành ” 😀
– Chúng ta cũng được dịp ôn lại một khẩu quyết rất hay dùng khi giải những bài toán về phương trình : “ Đưa phương trình đã cho về phương trình đã biết giải ” hay tư tưởng “ Quy lạ về quen ”– Cuối cùng, hãy ghi nhớ khẩu quyết này nhé và hãy dùng nó để “chiến đấu” với bất cứ “đối thủ” nào có chứa giai thừa mà bạn gặp. Nếu bạn muốn có thêm “đối thủ” để luyện tập hay gặp phải đối thủ mà “khẩu quyết” trên không thể “hạ gục được nó” thì hãy gõ yêu cầu của bạn vào hộp bình luận phía dưới đây. Chúc bạn luôn chiến thắng! 🙂
Thapsang.vn để nhận được thông báo khi có cập nhật mới.Mời bạn đón đọc những bài viết tiếp theo bằng cách đăng kí nhận bài viết mới qua email hoặc like fanpageđể nhận được thông tin khi có update mới .
Source: https://final-blade.com
Category : Kiến thức Internet