Chúng ta có thể định nghĩa dữ liệu (Data) là tất cả những gì được máy tính xử lý. Các loại dữ liệu cần tới máy tính xử lý có rất nhiều, tồn tại dưới nhiều dạng khác nhau về bản chất, về ý nghĩa, không riêng gì về số liệu mà còn là các kí tự, các mệnh đề logic, thể hiện qua các đối tượng cụ thể cần xử lý như tiền lương, địa chỉ, tên tuổi, văn bản, tín hiệu… Song nếu xét về phương diện điện tử thì máy tính chỉ hiểu các thông tin được biểu diễn dưới dạng mã nhị phân.Về phương diện ngôn ngữ bậc cao thì dữ liệu đã được khái quát hóa với các kiểu dữ liệu. Khi này, ta không cần quan tâm đến biểu diễn chi tiết trong máy tính của các kiểu dữ liệu.
Bạn đang đọc: Các Kiểu Dữ Liệu Là Gì – Kiểu Dữ Liệu Có Cấu Trúc
Một kiểu dữ liệu (Data Type) được định nghĩa với 2 điểm chính :Một kiểu dữ liệu ( ) được định nghĩa với 2 điểm chính :– Một tập hợp những giá trị mà một biến thuộc kiểu đó hoàn toàn có thể nhận được .– Trên đó xác lập một phép toán.
Cần nhớ rằng một biến phải gắn liền với một kiểu dữ liệu và chỉ một mà thôi. Trong ngôn từ Pascal, kiểu dữ liệu hoàn toàn có thể rất phức tạp nhưng nói chung đều được định nghĩa ra từ những kiểu đơn thuần nhất, không có cấu trúc .
Kiểu vô hướng (Scalar Type) hay kiểu đơn giản (Simple Type) là kiểu dữ liệu gồm một tập các giá trị của nó được sắp xếp theo một thứ tự tuyến tính. Chúng ta sẽ nghiên cứu kĩ hơn về kiểu vô hướng và các kiểu dữ liệu phức tạp khác. Trong phần tiếp theo, sẽ nói về 5 kiểu dữ liệu vô hướng đơn giản nhất, đã được định nghĩa sẵn và còn được gọi là kiểu đơn giản chuẩn (Simple Standar Type).
I – Kiểu dữ liệu Bun (Boolean: Đúng/Sai (True/False))
– Trước khi đi vào nghiên cứu các kiểu số nguyên và kiểu số thực quen biết, chúng ta hãy xét khái niệm kiểu Logic ( Boolean ). Trong thực tế chúng ta thường hay gặp loại đại lượng chỉ có hai giá trị : Đúng hoặc Sai. Ví dụ một mệnh đề, một câu hỏi, một phép toán… có thể được xem xét xem đúng hay sai. Ví dụ khi ta viết 3 – Trước khi đi vào nghiên cứu và điều tra những kiểu số nguyên và kiểu số thực quen biết, tất cả chúng ta hãy xét khái niệm kiểu Logic ( Boolean ). Trong trong thực tiễn tất cả chúng ta thường hay gặp loại đại lượng chỉ có hai giá trị : Đúng hoặc Sai. Ví dụ một mệnh đề, một thắc mắc, một phép toán … hoàn toàn có thể được xem xét xem đúng hay sai. Ví dụ khi ta viết 3
– Theo định nghĩa, một giá trị thuộc kiểu logic Boolean là một đại lượng nhận một trong hai giá trị Logic:TRUE(đúng) hoặc FALSE(sai). True và False là tên các giá trị đã được định nghĩa sẵn. Kiểu Boolean cũng đã định nghĩa sẵn quan hệ thứ tự False
+ Phép Or( phép “hoặc” logic )
+ Phép Not( phép “đảo” hay “phủ định” logic )
+ Phép Xor( phép “hoặc triệt tiêu” ).
False And True = FalseNot False = True
– Chúng ta có thể tóm tắt quy tắc thực hiện phép And và Or như sau :
+ Phép And chỉ cho kết quả là True khi và chỉ khi hai toán hạng đều là True.+ Phép And chỉ cho hiệu quả là True khi và chỉ khi hai toán hạng đều là True .+ Phép Or chỉ cho tác dụng là False khi và chỉ khi hai toán hạng đều là False .+ Phép Xor luôn luôn cho tác dụng là True khi hai toán hạng khác nhau. Còn nếu hai toán hạng giống nhau, Xor sẽ cho tác dụng làFalse.
* Hai vế của biểu thức so sánh phải cùng kiểu nhau ( trừ kiểu thực và nguyên ) và chúng có thể là các kiểu Real, Integer, Char, Boolean, Vô hướng do người sử dụng định nghĩa (sẽ học sau ).
Code:
* Hai vế của biểu thức so sánh phải cùng kiểu nhau ( trừ kiểu thực và nguyên ) và chúng hoàn toàn có thể là những kiểu Real, Integer, Char, Boolean, Vô hướng do người sử dụng định nghĩa ( sẽ học sau ). Code :
3 10 cho ta giá trị False
Cách viết 3
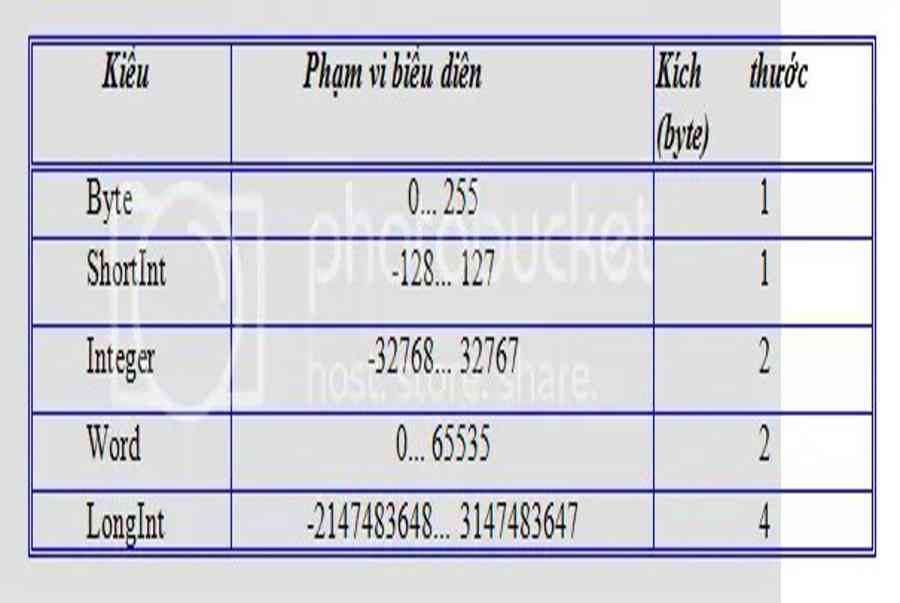
Một giá trị kiểu số nguyên là một thành phần của tập những số nguyên mà ta hoàn toàn có thể màn biểu diễn được trên máy, nghĩa là nó là một tập nhỏ của khoảng trống những số nguyên chứ không phải tổng thể mọi số nguyên đều hoàn toàn có thể giải quyết và xử lý trên máy tính được. Thông thường nhất, những số nguyên được màn biểu diễn bằng hai byte ( 16 bit ) nên khoanh vùng phạm vi của nó là từ – 32768 đến + 32767Các số nguyên được viết ra bằng những dãy chữ số 0, 1, 2, … 9 với chữ số đầu hoàn toàn có thể là dấu dương + hoặc dấu âm -, hoặc không có dấu.
Ví dụ :
Code:
Code :
+234, -32767, -1, 23
a) Các phép tính số học đối với số nguyên:
– Phép cộng và trừ : với kí hiệu là + và – như thường lệ.– Phép cộng và trừ : với kí hiệu là + và – như thường lệ .– Phép nhân : được kí hiệu bằng dấu * .Xem thêm : Trình Dược Viên Là Làm Gì ? Mô Tả Công Việc Trình Dược Viên Trình Dược Viên Là Gì– Phép chia : được kí hiệu bằng dấu / .– Phép chia lấy phần nguyên được thực thi với từ khóa Div.
Code:
Code:
14 Div 4 cho giá trị bằng 3
Ví dụ :
14 Mod 4 cho giá trị bằng 2
* Khi thực hiện các phép tính số học đối với số nguyên, cần hết sức thận trọng xem các phép toán đó có cho kết quả vượt ra khỏi phạm vi biểu diễn số nguyên của máy không.
* Khi thực thi những phép tính số học so với số nguyên, cần rất là thận trọng xem những phép toán đó có cho tác dụng vượt ra khỏi khoanh vùng phạm vi trình diễn số nguyên của máy không.
32000 + 800 – 2000 = 29200
b) Các phép tính quan hệ đối với số nguyên:
Các số nguyên có thể so sánh với nhau và với số thực qua các phép toán quan hệ như đã nói ở mục trước. Kết quả của phép toán quan hệ là kiểu Boolean tức là có giá trị True (Đúng) hoặc False (Sai).
Các số nguyên hoàn toàn có thể so sánh với nhau và với số thực qua những phép toán quan hệ như đã nói ở mục trước. Kết quả của phép toán quan hệ là kiểu Boolean tức là có giá trị True ( Đúng ) hoặc False ( Sai ).  ” / >
” / >
III – Kiểu số thực
1. Kiểu số thực ( Real ) :
Tương tự như định nghĩa kiểu số nguyên, kiểu số thực là tập hợp các số thực có thể biểu diễn được trong máy tính và được máy định nghĩa sẵn với từ khóa REAL.Tương tự như định nghĩa kiểu số nguyên, kiểu số thực là tập hợp những số thực hoàn toàn có thể trình diễn được trong máy tính và được máy định nghĩa sẵn với từ khóa REAL .
Các phép toán cộng (+), trừ (-), nhân(*), chia (/) cũng như các phép toán quan hệ (=,, , > =,
Do giá trị số thực có thể biểu diễn dưới dạng có dấu phẩy (hay dấu chấm) di động được nên người ta còn gọi đây là cách biểu diễn dấu phẩy động để phân biệt với cách biểu diễn số dưới dạng dấu phẩy tĩnh là cách biểu diển trong đó dấu phẩy cố định.
Do giá trị số thực hoàn toàn có thể màn biểu diễn dưới dạng có dấu phẩy ( hay dấu chấm ) di động được nên người ta còn gọi đây là cách trình diễn dấu phẩy động để phân biệt với cách trình diễn số dưới dạng dấu phẩy tĩnh là cách biểu diển trong đó dấu phẩy cố định và thắt chặt. 2. Mở rộng việc diễn đạt và khai báo số thực : ” / >
” / >
IV – Các hàm số học chuẩn
Các hàm sau đây được định nghĩa sẵn và được sử dụng với đối số là các số thực hoặc các số nguyên :
+ Abs(x): cho ta giá trị tuyệt đối của toán hạng x : | x |. Kiểu kết quả cùng kiểu với đối số, nghĩa là nếu x là thực thì Abs(x) cũng là số thực, nếu x là số nguyên thì Abs(x) cũng là số nguyên.Các hàm sau đây được định nghĩa sẵn và được sử dụng với đối số là những số thực hoặc những số nguyên :: cho ta giá trị tuyệt đối của toán hạng x : | x |. Kiểu hiệu quả cùng kiểu với đối số, nghĩa là nếu x là thực thì Abs ( x ) cũng là số thực, nếu x là số nguyên thì Abs ( x ) cũng là số nguyên .
+ Sqr(x): Cho giá trị bình phương của x. Kiểu kết quả cùng kiểu với đối số x.
+ Các hàm sau áp dụng cho đối số nguyên hoặc thực nhưng kết quả thì luôn luôn là kiểu thực :
– Sin(x), Cos(x), Arctan(x): là các hàm lượng giác bình thường.: là những hàm lượng giác thông thường .
– Sqrt(x): tính căn bậc hai của x.
– Succ(x): đối số nguyên n, cho số nguyên tiếp theo n, tức là n + 1.
– Pred(x): đối số nguyên n, cho số nguyên trước n, tức là n – 1.
– Odd(n): đối số nguyên n, True nếu n lẻ, False nếu n chẵn.
Việc chuyển một số thực sang số nguyên được thực hiện bởi 2 hàm chuẩn : hàm làm tròn và hàm cắt :Việc chuyển 1 số ít thực sang số nguyên được thực thi bởi 2 hàm chuẩn : hàm làm tròn và hàm cắt :
+ Hàm cắt Trunc(x) cho ta một số nguyên là phần nguyên của x, tức là cắt bỏ đi phần lẻ thập phân của x.Ví dụ : Trunc (3.146) = 3.
+ Hàm làm tròn Round(x) cho ta một số nguyên của x bằng cách qui tròn phần lẻ thập phân của x. Nói cách khác, Round(x) cho ta số nguyên gần với x nhất. Ví dụ : Round (56.678) = 57.
Có 2 hàm chuẩn là Ord và Chr cho phép thiết lập tương quan giữa bộ mã kí tự và một tập con các số tự nhiên
Có 2 hàm chuẩn là Ord và Chr cho phép thiết lập tương quan giữa bộ mã kí tự và một tập con các số tự nhiên
+ Ord( ) – Hàm Ord(‘c’) cho ta số thứ tự của kí tự ‘c’ trong bảng mã.
+ Chr( ) – Hàm Chr(n) cho ta kí tự có số thứ tự là n.
Hàm chuẩn Pred (trước) và Succ (tiếp theo sau) có thể áp dụng cho đối số là kí tự, kết quả là kí tự. Giả sử Ch là một kí tự nào đó, vậy thì :
+ Hàm chuẩn Pred ( Ch ) cho ta một kí tự nằm trước kí tự Ch trong bảng mã kí tự :
Source: https://final-blade.com
Category : Kiến thức Internet