Tóm Tắt

1. Nhắc lại kỹ năng và kiến thức mảng hai chiều

Một mảng hai chiều là một mảng chứa nhiều mảng một chiều, đôi lúc mảng hai chiều còn được ngầm hiểu như một bảng gồm có những hàng và những cột. Mảng hai chiều còn thường được gọi với cái tên là ma trận có kích cỡ M x N ( M là số hàng, N là số cột ) .

Truy cập vào thành phần trong mảng một chiều là việc truy vấn vào hàng thứ i cột thứ j có trong mảng. Ví dụ mảng a [ 1 ] [ 3 ] ( nghĩa là : i = 1, j = 3 )

Ví dụ dưới đây tôi có a là mảng 2 chiều (hay còn gọi là ma trận) có kích thước 3 x 3 như sau:

Bạn đang đọc: Con trỏ thao tác với mảng hai chiều trong C – Lập Trình Từ Đầu

#include 
int main()
{
    //khai bao mang 2 chieu a gom 3 x 3 phan tu
    int a[3][3] = {
        {1,2,3},
        {4,5,6},
        {7,8,9}
    };
}

Chúng ta hoàn toàn có thể tưởng tượng mảng hai chiều trên như một bảng như sau :

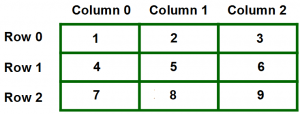
Như ở trên ta vẫn thường gọi mảng có những hàng và những cột, tuy nhiên bộ nhớ của máy tính là tuyến tính và không có hàng và cột. Vì lý do đó nên những thành phần của mảng 2 chiều thực ra được tàng trữ theo một hàng và được gom nhóm lại theo những cột có trong hàng, xem hình minh họa dưới đây để hiểu rõ hơn :

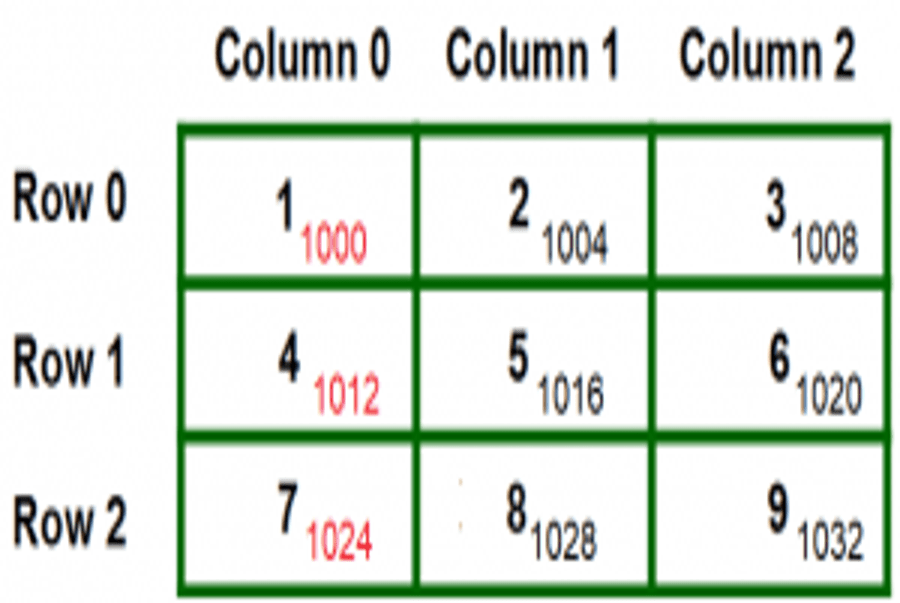
Dòng trên cùng là số lượng những hàng, vì tất cả chúng ta có mảng 2 chiều size 3 x 3 nên có 3 hàng ( 3 row ). Trong mỗi hàng được gom nhóm lại 3 thành phần tương ứng với 3 cột .
Dòng ở giữa là giá trị của mỗi thành phần ở hàng thứ i cột thứ j, ví dụ tại a [ 1 ] [ 3 ] = 3 ( nghĩa là i = 1, j = 3 ) hay a [ 2 ] [ 1 ] = 4 ( nghĩa là i = 2, j = 1 ) .
Dòng ở đầu cuối là địa chỉ của mỗi thành phần ở hàng thứ i cột thứ j, ví dụ a [ 1 ] [ 1 ] tàng trữ tại địa chỉ 1000, a [ 1 ] [ 2 ] tàng trữ tại địa chỉ 1004, a [ 1 ] [ 3 ] tàng trữ tại địa chỉ 1008 … và a [ 3 ] [ 3 ] tàng trữ tại địa chỉ 1032
Vì đây là mảng có kiểu int và có size 4 byte nên mỗi địa chỉ liền kề cách nhau 4 đơn vị chức năng ( 4 byte ) .

Chú ý: Địa chỉ ô nhớ trên chỉ là ví dụ để ta dễ hình dung.

2. Sử dụng con trỏ để thao tác với những thành phần trong mảng hai chiều

2.1 Địa chỉ ô nhớ của những thành phần mảng hai chiều

Mảng hai chiều hoàn toàn có thể được định nghĩa như thể một con trỏ trỏ tới một nhóm những mảng một chiều liên tục nhau .
Ở mảng một chiều ta biết rằng tên của mảng chứa địa chỉ của mảng đó, hay thành phần a [ 0 ] ( thành phần tiên phong ) cũng chứa địa chỉ của mảng đó .
Trong trường hợp của mảng 2 chiều, thành phần tiên phong trong mảng 2 chiều lại chính là một mảng 1 chiều và nếu mảng hai chiều a có size ( 3 x 3 ) và có địa chỉ tại thành phần tiên phong ( a + 0 ) là 1000 thì địa chỉ của thành phần thứ hai ( a + 1 ) là 1012, địa chỉ tại thành phần thứ ba ( a + 2 ) là 1024. Xem phần màu đỏ ở hình dưới đây :

Như vậy có nghĩa là :

(a + 0) trỏ đến mảng thứ 0
(a + 1) trỏ đến mảng thứ 1
(a + 2) trỏ đến mảng thứ 2

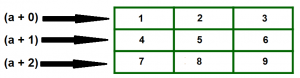
Tóm lại, ta hoàn toàn có thể hiểu ( a + i ) trỏ đến mảng một chiều thứ i trong mảng 2 chiều .
Tuy nhiên, trong mảng thứ i lại sống sót thêm những giá trị ở trong đó ( vì mảng thứ i này là mảng 1 chiều ). Ví dụ ( a + 0 ) thì sẽ là :

Hay ( a + 1 ) thì sẽ là :

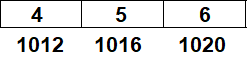
Hoặc ( a + 2 ) thì sẽ là :

Chú ý: Địa chỉ ô nhớ trên chỉ là ví dụ để ta dễ hình dung.

2.2 Sử dụng con trỏ để truy vấn địa chỉ và giá trị của thành phần mảng hai chiều

Bạn đọc hãy cùng tôi tìm hiểu thêm hai ví dụ dưới đây để rút ra công thức tổng quát cho việc lấy địa chỉ và giá trị của mảng hai chiều a [ i ] [ j ]
Ví dụ 1, giả sử tôi muốn lấy địa chỉ của a [ 0 ] [ 0 ], nghĩa là tôi truy vấn vào mảng 1 chiều tiên phong, và truy vấn tiếp theo vào thành phần tiên phong trong mảng đó. Xem hình minh họa bên dưới

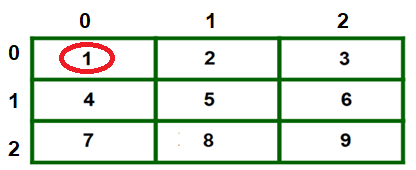
Tôi sẽ sử dụng cú pháp : * ( a + 0 ) + 0 để lấy địa chỉ a [ 0 ] [ 0 ]

#include 
int main()
{
    //khai bao mang 2 chieu a gom 3 x 3 phan tu
    int a[3][3] = {
        {1,2,3},
        {4,5,6},
        {7,8,9}
    };
    //lay dia chi a[0][0] bang *(a + 0) + 0
    printf("Dia chi cua a[0][0] la: %x", *(a + 0) + 0);
}

Dia chi cua a[0][0] la: 62fdf0

Chú ý: Địa chỉ ô nhớ trên mỗi máy tính khi thực thi chương trình trên là khác nhau. Kết quả trên chỉ là minh họa

Ví dụ thứ 2 tôi muốn lấy địa chỉ của a[2][1], nghĩa là tôi truy cập vào mảng 1 chiều thứ 2, và truy cập tiếp theo vào phần tử thứ 1 trong mảng đó.

Xem thêm: Các kiểu dữ liệu trong Java

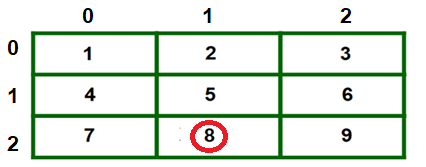
Tôi sẽ sử dụng cú pháp : * ( a + 2 ) + 1 để lấy địa chỉ a [ 2 ] [ 1 ]

#include 
int main()
{
    //khai bao mang 2 chieu a gom 3 x 3 phan tu
    int a[3][3] = {
        {1,2,3},
        {4,5,6},
        {7,8,9},
    };
    //lay dia chi a[2][1] bang *(a + 2) + 1
    printf("Dia chi cua a[2][1] la: %x", *(a + 2) + 1);
}

Dia chi cua a[2][1] la: 62fe0c

Chú ý: Địa chỉ ô nhớ trên mỗi máy tính khi thực thi chương trình trên là khác nhau. Kết quả trên chỉ là minh họa

→ Qua hai ví dụ trên ta hoàn toàn có thể rút ra công thức cho địa chỉ và giá trị của thành phần a [ i ] [ j ] nào đó trong mảng 2 chiều

Công thức cho địa chỉ ô nhớ a[i][j] là: *(a+i)+j
Và ta hoàn toàn lấy được giá trị của a[i][j] bằng cách thêm toán tử * cho toàn bộ công thức trên: *(*(a+i) + j)

Để minh họa về việc lấy giá trị của tất cả chúng ta cùng quay lại ví dụ 2, tôi sẽ lấy giá trị tại a [ 2 ] [ 1 ] = 8

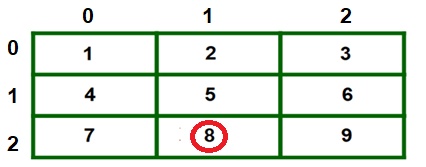
Theo công thức *(*(a+2) + 1)

#include 
int main()
{
    //khai bao mang 2 chieu a gom 3 x 3 phan tu
    int a[3][3] = {
        {1,2,3},
        {4,5,6},
        {7,8,9},
    };
    //lay gia tri a[2][1] bang *(*(a+2) + 1)
    printf("Gia tri cua a[2][1] la: %d",*(*(a+2) + 1));
}

Gia tri cua a[2][1] la: 8

Như vậy, ta đã có công thức cho địa chỉ ô nhớ và giá trị của thành phần a [ i ] [ j ] trong mảng hai chiều .
Tiếp theo ta sẽ vận dụng con trỏ để truy vấn vào địa chỉ và giá trị của thành phần mảng a [ i ] [ j ] đó. Ta nhớ lại rằng mảng 1 chiều khi thao tác với con trỏ ta chỉ việc gán con trỏ p = a ( trong đó a là tên mảng ) bạn đọc quên hoàn toàn có thể quay lại đọc Bài 2 : Con trỏ thao tác với mảng một chiều trong C .
Luôn nhớ rằng, mảng hai chiều thực ra cũng là mảng 1 chiều chứa nhiều thành phần và mỗi thành phần trong đó lại là một mảng 1 chiều gồm nhiều cột .
Vì thế để sử dụng con trỏ tàng trữ địa chỉ của mảng 2 chiều đó ta cần một con trỏ đến một mảng có size bằng số cột của mảng 1 chiều .
Ví dụ dưới đây tôi có mảng a [ 3 ] [ 3 ] ( có 3 hàng 3 cột ) nên tôi sẽ khai báo như sau :

#include 
int main()
{
    //khai bao mang 2 chieu a gom 3 x 3 phan tu
    int a[3][3] = {
        {1,2,3},
        {4,5,6},
        {7,8,9},
    };
    //khoi tao con tro p tro den 3 cot
    int (*p)[3];
    //gan con tro p bang mang a
    p = a;
}

Giả sử tôi có mảng a [ 3 ] [ 4 ] ( 3 hàng 4 cột ) tôi sẽ khai báo : int ( * p ) [ 4 ] ;

→ Như vậy ta có công thức để có thể gán con trỏ cho mảng 2 chiều có kích thước a[i][j] là: int (*p)[j]

Bây giờ, ta trọn vẹn hoàn toàn có thể sử dụng con trỏ để lấy giá trị và địa chỉ của những thành phần trong mảng a bằng cách :

(p + i) để lấy ra địa chỉ của các phần tử trong mảng hai chiều
* ( * ( p + i) + j ) để lấy ra giá trị của các phần tử trong mảng

Ví dụ dưới đây tôi sẽ sử dụng con trỏ ( * p ) [ 3 ] để lấy giá trị và địa chỉ của mảng a [ 3 ] [ 3 ]

#include 
int main()
{
    //khai bao mang 2 chieu a gom 3 x 3 phan tu
    int a[3][3] = {
        {1,2,3},
        {4,5,6},
        {7,8,9},
    };
    //khoi tao con tro p
    int (*p)[3];
    //gan con tro p bang mang a
    p = a;
    
    //duyet cac hang trong mang
    for(int i = 0; i < 3; i ++){
        //hien thi dia chi cua tung phan tu trong mang 2 chieu
        printf("Dia chi phan tu %d la: %x \n",i, p + i);
        //duyet cac cot trong mang
        for(int j = 0; j < 3; j++){
            //hien thi gia tri cua tung phan tu
            printf ("Gia tri: a[%d][%d] =%d \n",  i,  j,  * (  * ( p  +  i)  +  j ) );
        }   
        printf("\n \n");
    }
}

Dia chi phan tu 0 la: 62fde0 Gia tri : a [ 0 ] [ 0 ] = 1 Gia tri : a [ 0 ] [ 1 ] = 2 Gia tri : a [ 0 ] [ 2 ] = 3 Dia chi phan tu 1 la : 62 fdec Gia tri : a [ 1 ] [ 0 ] = 4 Gia tri : a [ 1 ] [ 1 ] = 5 Gia tri : a [ 1 ] [ 2 ] = 6 Dia chi phan tu 2 la : 62 fdf8 Gia tri : a [ 2 ] [ 0 ] = 7 Gia tri : a [ 2 ] [ 1 ] = 8 Gia tri : a [ 2 ] [ 2 ] = 9

Ví dụ 2 tôi sử dụng con trỏ ( * p ) [ 3 ] để lấy giá trị những thành phần là số chẵn có trong mảng a

#include 
int main()
{
    //khai bao mang 2 chieu a gom 3 x 3 phan tu
    int a[3][3] = {
        {1,2,3},
        {4,5,6},
        {7,8,9},
    };
    //khoi tao con tro p cho mang a[3][3]
    int (*p)[3];
    //gan con tro p bang mang a
    p = a;
    
    printf("Cac phan tu trong mang la so chan \n");
    //duyet cac hang trong mang
    for(int i = 0; i < 3; i ++){
        //duyet cac cot trong mang
        for(int j = 0; j < 3; j++){
            if(* (  * ( p  +  i)  +  j ) % 2 == 0){
                //hien thi gia tri cac phan tu la so chan
                printf ("Gia tri: a[%d][%d] =%d \n",  i,  j,  * (  * ( p  +  i)  +  j ) );
            }
        }   
    }
}

Cac phan tu trong mang la so chan

Gia tri: a[0][1] =2

Xem thêm: Vòng lặp – while vs for trong Javascript – NordicCoder

Gia tri : a [ 1 ] [ 0 ] = 4
Gia tri : a [ 1 ] [ 2 ] = 6
Gia tri : a [ 2 ] [ 1 ] = 8

Source: https://final-blade.com
Category: Kiến thức Internet

admin

final-blade.com