Đệ quy trong C – Hàm đệ quy và tính dừng của đệ quy

Posted on Updated on by adminChuyên mục:Kiến thức Internet
This entry is part 28 of 69 in the series This entry is part 28 of 69 in the series Học C Không Khó

Hàm đệ quy trong C là các hàm mà bản thân nó có khả năng gọi lại chính nó. Và kỹ thuật này được gọi là đệ quy. Trong bài học này, Lập Trình Không Khó sẽ cùng các bạn đi tìm hiểu về hàm đệ quy, bao gồm: tính chất của hàm đệ quy, ưu điểm và nhược điểm của đệ quy, thực hành các bài toán kinh điển sử dụng đệ quy, tìm hiểu về khái niệm khử đệ quy…

Hàm đệ quy trong C hoạt động ra sao?

Dưới đây là một chương trình minh họa sử dụng đệ quy trong C. Bạn chú ý, trong thân hàm recurse() có lời gọi hàm tới chính nó => đó là hàm đệ quy.

01234567891011121314

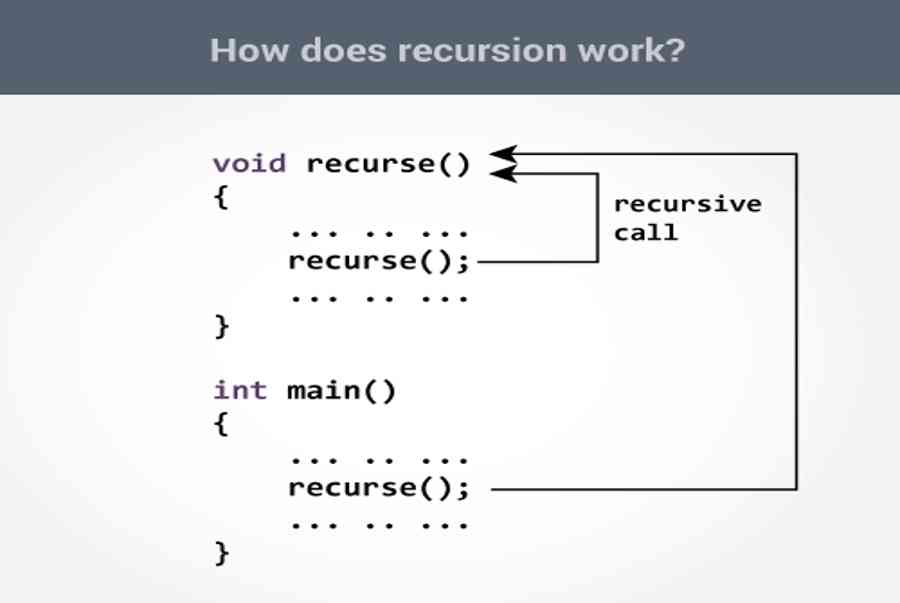
voidrecurse()

{

……..

recurse();

……..

}

intmain()

{

……..

recurse();

……..

}

Vậy 1 chương trình sẽ chạy thế nào nếu có hàm đệ quy ? Bạn hãy xem hình ảnh dưới đây :
Bài 30. Đệ quy trong C - Hàm đệ quy
Như những bạn hoàn toàn có thể thấy, khi một hàm đệ quy được gọi ( ở ví dụ trên là hàm main gọi ) thì thay vì hàm đó chỉ được thực thi 1 lần thì ở đây bản thân hàm gọi lại chính nó => Nó hoàn toàn có thể tự chạy lại chính mình số lần bất kể .

Tính dừng là gì?

Chắc hẳn bạn đang có câu hỏi, hàm đệ quy tự gọi lại chính nó ở mỗi lần chạy; Vậy thì nó chạy không bao giờ dừng à? Để tránh việc lặp vô tận, hàm đệ quy cần có tính dừng: Nếu gặp 1 điều kiện nào đó, nó cần phải dừng lại việc tự gọi lại chính mình. Và tính dừng là điều bắt buộc phải có trong 1 hàm đệ quy trong C cùng như mọi ngôn ngữ khác.

Bạn vui vẻ xem video phía trên để thấy rõ hơn về tính dừng của đệ quy. Sau đây, tất cả chúng ta sẽ cùng nhau đi giải những bài tập tầm cỡ sử dụng đệ quy. Mình sẽ lý giải cụ thể ở mỗi ví dụ nhé !

Bài tập thực hành đệ quy trong C

BT1. Tính tổng các số từ 1 đến n

0123456789101112131415161718192021222324252627282930313233343536

#include

/ / Hàm đệ quy

intSumRecursion(intn){

/ *

sum = 1 + … + n

* /

/ / Cái if này là điều kiện kèm theo dừng

if(n==0){

return0;

}

returnn+SumRecursion(n-1);/ / Gọi lại chính nó

}

/ *

Giải thích hàm đệ quy

Giả sử n = 4

4 + SumRecursion ( 3 )

4 + 3 + SumRecursion ( 2 )

4 + 3 + 2 + SumRecursion ( 1 )

4 + 3 + 2 + 1 + SumRecursion ( 0 )

4 + 3 + 2 + 1 + 0

* /

intmain(){

intn;

printf(” \ nNhap n = “);

scanf(” % d “,và n ) ;

intsum2=SumRecursion(n);

printf(” \ nSum1 = % d “,sum1);

printf(” \ nSum2 = % d “,sum2);

}

Bài tập này được lý giải cụ thể trên video rồi, do đó mình chỉ làm rõ hai yếu tố ở đây :

  • Đệ quy: Hàm SumRecursion() đã gọi lại chính nó với 1 tham số khác
  • Tính dừng: Khi tham số truyền vào có giá trị là 0 thì sẽ dừng gọi đệ quy => Vì gặp return là thoát hàm mất rồi.
  • Giải thích lần lượt các bước gọi hàm, cách hàm thực hiện có trong code và video phía trên.

BT2. Xây dựng vòng lặp bằng đệ quy

Do đệ quy có đặc thù lặp, nên bạn trọn vẹn hoàn toàn có thể dùng đệ quy để làm vòng lặp. Ví dụ như sau :

01234567891011121314151617

#include

staticintcount=0;

voidloop(){

count++;

if(count<=5){

printf(” loop % d \ n “,count);

loop();

}

}

intmain(){

loop();

return0;

}
  • Tính dừng: Nếu count <= 5 sai, hàm sẽ dừng lại. Bởi vì lời gọi đệ quy chỉ được thực hiện khi điều kiện này đúng.
  • Việc sử dụng biến static trong C,  bạn sẽ được tìm hiểu rõ nó trong bài học số 32 của khóa học này. Biến static sẽ không bị reset giá trị nên chúng ta có thể dùng nó để đếm.

Chú ý: Nếu hàm đệ quy không có điều kiện dừng, nó sẽ lặp vô tận! Bạn có thể chạy thử ví dụ dưới đây nhé.

0123456789101112

#include

voidloop(){

printf(" loop \ n ");

loop();

}

intmain(){

loop();

return0;

}
01234567

intDigitCount(intn)

{

if(n==0)

return0;

return1+DigitCount(n/10);

}
  • Giải thích: Chừng nào mà số n còn lớn hơn 0, chúng ta sẽ tăng giá trị đếm 1 đơn vị, và sau đó chia nguyên n với 10 để bỏ chữ số cuối của nó.

BT4. Tìm UCLN của 2 số nguyên dương

0123456789101112131415

/ *

Vì dụ : a = 9, b = 3

Vì a * b ! = 0 => return UCLN ( 0, 3 ) / / ULCN ( 9 % 3, 3 )

Vì a * b = = 0 => return a + b = 3

* /

intUCLN(inta,intb)

{

if(a *b==0)

returna+b;

if(a>b)

returnUCLN(a-b,b);

else

returnUCLN(a,b-a);

}

Các bạn sẽ liên tục được thực hành thực tế những bài tập về hàm và hàm đệ quy ở những bài học kinh nghiệm tiếp theo. Xin chào và hẹn gặp lại cả nhà !

admin