Tìm hiểu thuật toán sắp xếp trộn Merge Sort, ý tưởng thuật toán, giải thuật, ưu nhược điểm và đánh giá độ phức tạp. Cài đặt thuật toán merge sort bằng code C/C++, java. .. tất cả sẽ có trong bài viết này nhé!
Tóm Tắt
1. Merge sort là gì?
Sắp xếp trộn – Merge Sort là một thuật toán sắp xếp thuộc loại sắp xếp nhanh trong khoa học máy tính. Merge sort là thuật toán điển hình cho tư tưởng chia để trị để giải quyết các bài toán có dữ liệu lớn và phức tạp. Cụ thể với bài toán sắp xếp, nó sẽ chia nhỏ danh sách cần sắp xếp thành từng phần tử rời sau đó hòa nhập theo phương pháp trộn tự nhiên thành dãy có thứ tự.
Một chút về lịch sử, Merge sort là một trong những phương pháp đầu tiên sử dụng trong bài toán sắp xếp. Thuật toán này được đề xuất bởi John Von Neumann vào đầu năm 1945. Một cuộc thảo luận và phân tích chi tiết về sắp xếp hợp nhất đã được xuất hiện trong một báo cáo của Goldstine và Neumann như đầu năm 1948.
Đây là một trong những thuật toán sắp xếp so sánh cực kỳ phổ cập do đó hãy bổ trợ kiến thức và kỹ năng về nó tối thiểu là ý tưởng sáng tạo thuật toán, biết đâu sau này nó sẽ giúp ích cho việc làm của bạn. Mình sẽ nỗ lực trình diễn cụ thể nhất hoàn toàn có thể để giúp bạn dễ hiểu nó nha .
Xem thêm các thuật toán sắp xếp thông dụng khác tại đây.
2. Ý tưởng sắp xếp trộn
Các thuật toán sắp xếp đơn thuần như Bubble Sort, Insertion Sort. .. đều không hề giải quyết và xử lý được tài liệu lớn. Thuật toán sắp xếp trộn lấy sáng tạo độc đáo từ việc chia để trị để chia nhỏ bài toán thành những bài toán nhỏ hơn, sau đó xử lý chúng. Từ đó sẽ giúp giải quyết và xử lý tài liệu lớn một cách tốt hơn, tối ưu về mặt thời hạn .
Ý tưởng đưa ra như sau:
- Chia danh sách gồm n phần tử chưa được sắp xếp thành n danh sách con, mỗi danh sách chứa một phần tử (danh sách một phần tử được coi là đã sắp xếp).
- Liên tục hợp nhất các danh sách con để tạo ra các danh sách con được sắp xếp mớ cho đến khi chỉ còn lại một danh sách. Đây sẽ là danh sách được sắp xếp.
Khi triển khai code, ta sẽ cụ thể hóa bằng các bước:
Bước 1:
- Chia dãy cần sắp xếp thành 2 dãy con
- Từ dãy con thu được lại tiếp tục chia thành 2 dãy con nhỏ hơn nữa
- Quá trình phân chia tiếp tục cho đến khi thu được dãy con chỉ còn duy nhất 1 phần tử.
Bước 2:
- Hòa nhập 2 dãy con nhỏ nhất thành dãy con lớn hơn sao cho đúng thứ tự
- Từ hai dãy con lớn hơn lại hòa nhập thành 2 dãy con lớn hơn nữa….
- Quá trình hòa nhập cứ tiếp tục như vậy cho đến khi thu được dãy số ban đầu đã được sắp xếp.
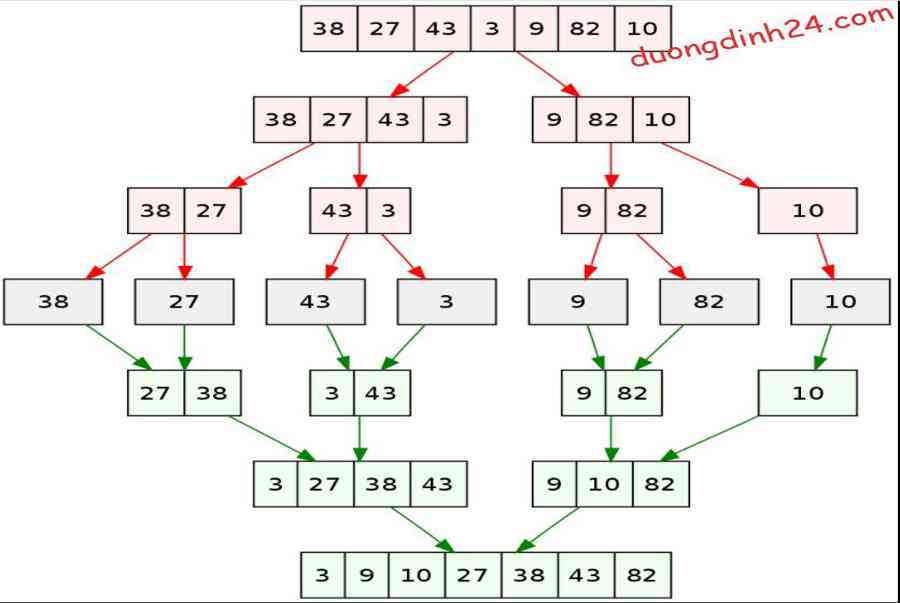
Để dễ hình dung, bạn nhìn hình sau nhé:
Hình minh họa merge sortBạn hoàn toàn có thể truy vấn vào hackereath.com để tìm hiểu thêm animation của thuật toán nhé !
Lưu đồ thuật toán sắp xếp trộn:
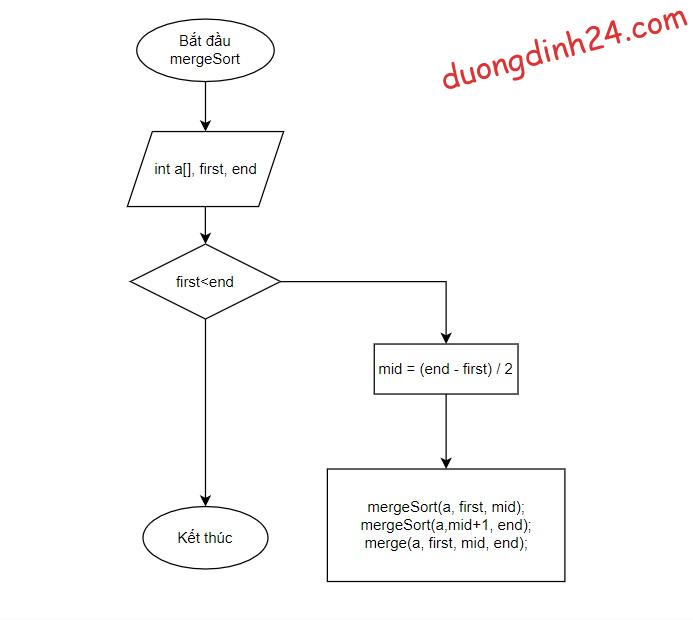Lưu đồ thuật toán
3. Cài đặt thuật toán Merge sort
Với giải thuật nêu trên, ta cần thiết kế hai hàm, một hàm dùng để chia nhỏ list làm thân hàm Merge sort, một hàm dùng để trộn hai list con lại với nhau .
Trộn hai dãy con hay còn gọi là hòa nhập hai dãy con là trái tim quan trọng nhất của giải thuật. Có lẽ đây là nguyên do mà người ta gọi nó là sắp xếp trộn .
3.1 Hàm trộn – merge C/C++
Chú ý: Bài viết của mình thực hiện sắp xếp tăng dần nhé!
Hàm trộn sẽ ghép hai dãy con lại thành một dãy có thứ tự, dãy con nhỏ nhất ta cần ghép sẽ có 1 thành phần. Thực chất đó là ghép hai mảng liền nhau đã sắp xếp thành một mảng có thứ tự .
Ta sẽ viết hàm trộn trực tiếp trên dãy khởi đầu và khai báo thêm 2 mảng trung gian ( left, right ) để lưu và trộn. Do đó sẽ là trộn hai dãy con liền kề nhau .
Ý tưởng:
- Tham số truyền vào gồm: mảng a, vị trí bắt đầu start, vị trí trung gian mid chia hai mảng con, vị trí cuối cùng của mảng
- Duyệt cùng lúc 2 mảng con trung gian, tìm ra phần tử nhỏ hơn rồi điền vào mảng chính
- Khi một mảng con đã hết, cho phần tử còn lại của mảng con chưa hết vào mảng chính
Code C / C + +
/* Hàm trộn - merge
start - chỉ số bắt đầu mảng
mid - chỉ số giữa, chia đôi mảng
*/
void merge(int a[], int start, int mid, int end){
int n1 = mid - start + 1; // Số phần tử mảng con trái
// + 1 là do lưu thêm phần tử ở vị trí mid
int n2= end-mid; // Số phần tử mảng con phải
int left[n1]; int right[n2]; // Khai báo hai mảng trung gian
// Copy giữ liệu từ mảng chính ra hai mảng con
for(int x=0; x=right[j]){ // Nếu phần tử mảng con trái >= mảng con phải
a[k]=right[j]; // Điển phần tử mảng con phải vào mảng chính
j++; // xét phần tử tiếp theo của mảng right
}
else{ // Ngược lại tức là left[i] < right[j]
a[k]=left[i];
i++;
}
k++; // Tăng index của mảng chính, mỗi lần lặp sẽ tìm được 1 phần tử thích hợp
}
// Sau vòng lặp trên, 1 trong 2 mảng đã duyệt hết phần tử, hoặc cả hai cùng hết
while(j
3.2 Hàm mergeSort
Phần này có sử dụng giải thuật đệ quy trong lập trình, nếu bạn chưa biết nó có thể tham khảo tại đây.
Hàm mergeSort sẽ triển khai :
- Chia nhỏ mảng ban đầu thành 2 mảng con.
- Thực hiện đệ quy mergeSort hai mảng con đó.
- Cuối cùng thì trộn hai mảng con lại bằng hàm merge đã viết ở trên
Hàm mergeSort C / C + + :
// merge
//void merge(int a[], int start, int mid, int end){.. .}
// MergeSort
void mergeSort(int a[], int first, int end){
int t; // biến để lưu vị trí chia đôi mảng
if(first
Để hàm sắp xếp hoàn toàn có thể hoạt động giải trí được, bạn cần ghép hai hàm ở mục 3.1 và 3.2 lại nhé !
4. Đánh giá thuật toán sắp xếp trộn – Mergesort
Bảng đánh giả thuật toán:
Trường hợp Độ phức tạp Bộ nhớ sử dụng Tốt nhất O (n log n) n Trung bình O (n log n) n Xấu nhất O(n log n) n
Ưu điểm:
- Độ phức tạp trung bình O(n log n), tốc độ giải quyết khá nhanh
- Có tính ổn định và thích ứng, tốc độ không bị ảnh hưởng nhiều bởi dữ liệu đầu vào
- Xử lý khá tốt với dữ liệu lớn đặc biệt là dạng list, file
Nhược điểm:
- Tốn nhiều bộ nhớ nếu sử dụng đệ quy
- Code khó cài đặt, tương đối phức tạp
- Trong hầu hết các trường hợp, thuật toán này không được đánh giá cao hơn Quick sort
Lời kết: Bài viết này mình có tham khảo và tổng hợp từ nhiều nguồn khác nhau như Wikipedia, rất mong nhận được góp ý từ phía bạn đọc để nó được trở nên hoàn thiện hơn.
Cảm ơn bạn đã ghẽ thăm blog của mình nhé ^ ^ .
Source: https://final-blade.com
Category: Kiến thức Internet
