Tìm hiểu thuật toán sắp xếp nhanh Quick sort, ý tưởng, ưu nhược điểm, độ phức tạp của thuật toán. Cách cài đặt minh họa thuật toán quicksort bằng C/C++. Cùng tiếp tục series các bài viết về thuật toán của mình nhé!
Tóm Tắt
1. Sắp xếp nhanh – Quick sort là gì?
Thuật toán sắp xếp nhanh hay còn gọi là QuickSort Algorithm là một trong 6 thuật toán sắp xếp thông dụng nhất của khoa học máy tính. Thuật toán sử dụng tư tưởng chia để trị nên còn được ví là part sort và thuộc loại sắp xếp phức tạp. Từ dãy ban đầu, người ta sẽ chia dãy thành hai phần nhỏ theo một quy tắc xác định, từ đó giúp cải thiện tốc độ của việc săp xếp.
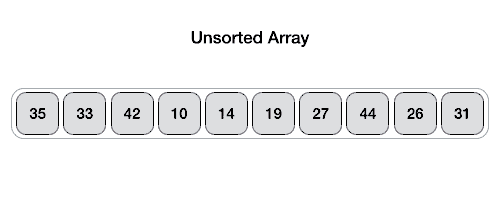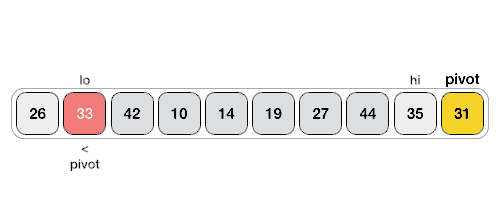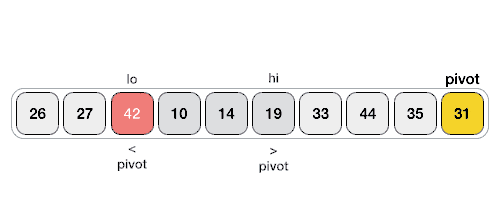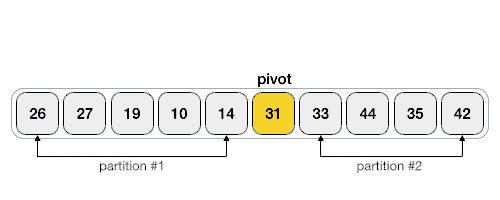 Hình minh họa Quick sort
Hình minh họa Quick sort
Thuật toán sắp xếp nhanh được phát triển vào năm 1959 bởi Tony Hoare khi ông đang là sinh viên thỉnh giảng tại Đại học Tổng hợp Moscow. Khi đó, Hoare đang thực hiện một dự án về máy dịch cho Phòng thí nghiệm Vật lý Quốc gia. Là một phần của quá trình dịch thuật, ông phải sắp xếp các từ của các câu tiếng Nga trước khi tra cứu chúng trong từ điển Nga-Anh đã được sắp xếp theo thứ tự bảng chữ cái và được lưu trữ trong băng từ. Để hoàn thành nhiệm vụ này, ông đã phát hiện ra Quick Sort và sau đó đã xuất bản mã năm 1961.
Bạn đang đọc: Thuật toán sắp xếp nhanh – Quick Sort Algorithm C/C++
Quick Sort là thuật toán đáng được chăm sóc và thực sự rất quan trọng. Hầu hết trong những thư viện của những ngôn từ lập trình lúc bấy giờ đều có sẵn thuật toán này. Bạn cũng hãy để nó trong thư viện trí não của mình nhé !
2. Ý tưởng thuật toán
Quicksort là thuật toán ứng dụng ý tưởng chia nhỏ để trị. Đầu tiên nó chia mảng đầu vào thành hai mảng con một nửa nhỏ hơn, một nửa lớn hơn dựa vào một phần tử trung gian. Sau đó, nó sắp xếp đệ quy các mảng con để giải quyết bài toán.
Mấu chốt của thuật toán ở việc chia mảng con hay còn gọi là thuật toán phân đoạn. Cách xử lý hoàn toàn có thể tóm tắt như sau :
- Chọn một phần tử trong mảng làm phần tử trung gian để chia đôi mảng gọi là pivot. Thông thường ta thường chọn phần tử đầu tiên, phần tử ở giữa mảng hoặc phần tử cuối cùng của mảng để làm pivot.
- Phân đoạn: di chuyển phần tử có giá trị nhỏ hơn pivot về một bên, tất cả các phần tử có giá trị lớn hơn pivot xếp về một bên (các giá trị bằng pivot có thể đi theo một trong hai cách).
- Sau bước phân đoạn di chuyển pivot về đúng vị trí giữa của 2 mảng con
- Áp dụng đệ quy các bước phân đoạn trên cho hai mảng con để thực hiện sắp xếp
Trường hợp dừng của đệ quy là khi những mảng con có kích cỡ bằng 0 hoặc 1, khi đó nó đã được sắp xếp theo định nghĩa, vì thế chúng không khi nào cần phải sắp xếp .
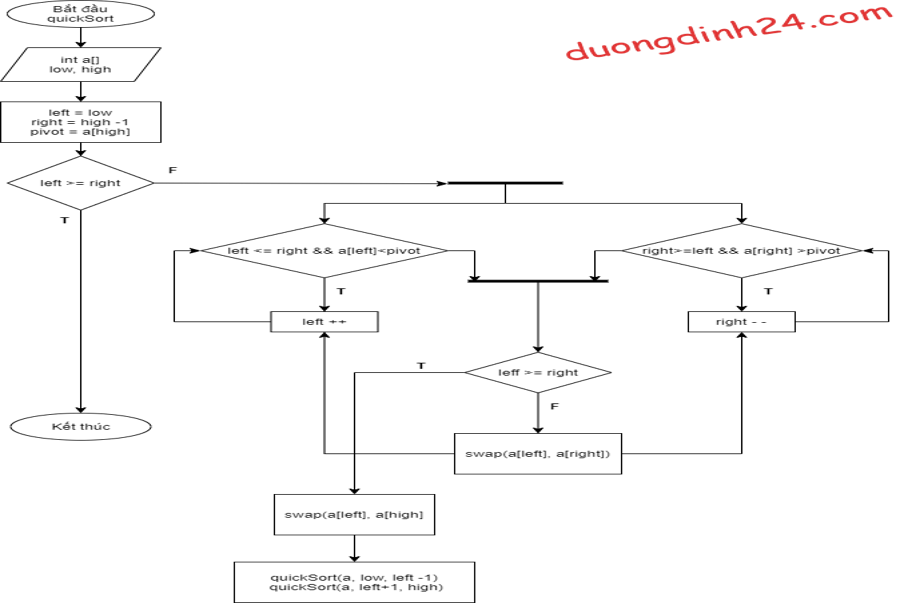
Lưu đồ thuật toán sắp xếp nhanh:
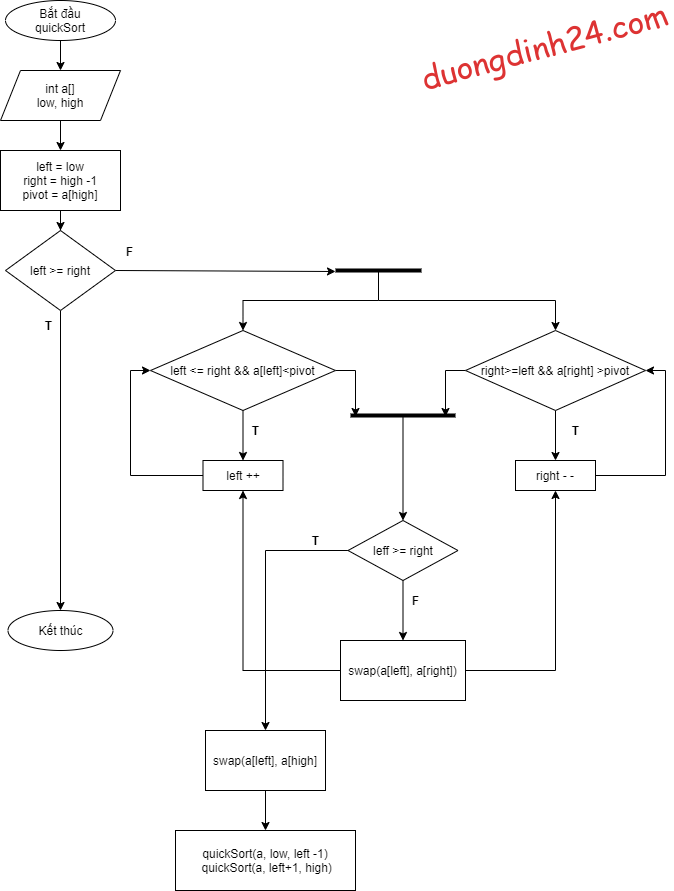 Lưu đồ thuật toán
Lưu đồ thuật toán
3. Cài đặt thuật toán Quick Sort C/C++
Như đã nói ở phần trên, việc phân đoạn chính là việc quan trọng nhất. Bạn hoàn toàn có thể thiết kế xây dựng thuật toán phân đoạn riêng hoặc hoàn toàn có thể viết chung luôn với quickSort trong cùng một hàm đều được. Để dễ hiểu mình sẽ viết riêng thành hai hàm riêng không liên quan gì đến nhau .
Có 3 cách chọn pivot ( thành phần làm chốt ), mục tiêu là để chọn được thành phần có giá trị trung gian để chia làm hai vế cho list .
- Chọn phần tử đầu mảng
- Chọn phần tử ở giữa mảng
- Chọn phần tử cuối mảng
Bài viết này mình sẽ chọn thành phần ở cuối làm chốt và setup bằng ngôn từ C / C + +
3.1 Thuật toán phân đoạn
Hàm phân đoạn ở phía dưới viết với sáng tạo độc đáo :
- Có 3 tham số truyền vào: mảng a, low, high. low và hight lần lượt là chỉ số đầu và chỉ số cuối
- Chia mảng thành 2 phần: bên trái nhỏ hơn pivot, bên phải lớn hơn pivot
- Chọn pivot là phần tử cuối cùng: pivot = a[high];
- lef chỉ sổ đầu của mảng: left = low;
- right chỉ số cuối của mảng trừ pivot: right = high – 1;
Thực hiện vòng lặp trong khi left < right như sau :
- Trong khi left <= right và a[left] < pivot: left++;
(tìm tới vị trị a[left] > pivot) - Trong khi right >= left và a[right] > pivot: right –;
(tìm tới vị tri a[right]) - Khi tìm được vị trí của left, right thích hợp, tức là ( a[left] > pivot và a[right] < pivot):
swap(a[left], a[right]);
Cuối cùng là chuyển pivot về giữa mảng: swap(a[left], a[high]);
// Hàm phân đoạn
int partition(int a[], int low, int high){
int pivot = a[high]; // Chọn pivot là phần tử cuối cùng
int right = high-1, left = low; // Chọn left, right
while(true){ // Trong khi còn đúng (left < right)
while(left<=right && a[left]=left && a[right]>pivot) right--; // Tìm right thích hợp
if(left>=right) // left >= right dừng
break;
swap(a[left], a[right]); // Đổi chỗ
left++; // Xét phần tử tiếp theo
right--;
}
swap(a[left], a[high]); // Đổi chỗ pivot về giữa mảng
return left; // Trả về vị trí của pivot
}
// Hàm đổi giá trị hai phần tử
void swap(int &a, int &b){
int temp;
temp = a;
a = b;
b = temp;
}
Hàm quickSort C/C++ full:
// Hàm phân đoạn
int partition(int a[], int low, int high){
int pivot = a[high]; // Chọn pivot là phần tử cuối cùng
int right = high-1, left = low; // Chọn left, right
while(true){ // Trong khi còn đúng (left < right)
while(left<=right && a[left]=left && a[right]>pivot) right--; // Tìm right thích hợp
if(left>=right) // left >= right dừng
break;
swap(a[left], a[right]); // Đổi chỗ
left++; // Xét phần tử tiếp theo
right--;
}
swap(a[left], a[high]); // Đổi chỗ pivot về giữa mảng
return left; // Trả về vị trí của pivot
}
// Hàm quick sort
void quickSort(int a[], int low, int high){
if(low < high) //Mảng có nhiều hơn 0 phần tử
{
int pivot = partition(a, low, high); // Chia đôi mảng
quickSort(a,low, pivot-1); // Đệ quy bên trái
quickSort(a, pivot+1, high); // Đệ quy bên phải
}
}
// Hàm đổi giá trị hai phần tử
void swap(int &a, int &b){
int temp;
temp = a;
a = b;
b = temp;
}
3.2 Hàm Quick Sort full
Quick sort có sử dụng giải thuật đệ quy, nếu bạn chưa biết đệ quy là gì hoàn toàn có thể tìm hiểu thêm tại đây .
void quickSort(int a[], int low, int high){
if(low < high) //Mảng có nhiều hơn 0 phần tử
{
int pivot = partition(a, low, high); // Chia đôi mảng
quickSort(a,low, pivot-1); // Đệ quy bên trái
quickSort(a, pivot+1, high); // Đệ quy bên phải
}
}
Code quickSort kết hợp phân đoạn C/C++:
(ghép hàm phân đoạn và quicksort vào 1 hàm).
// Low là vị trí đầu mảng, high là vị trí cuối mảng
public void quickSort(int a[], int low, int high)
{
if (low >= high) // Khi đó mảng có 0 phần tử, dừng
return;
else
{
int pivot = a[high]; // Chọn phần tử cuối làm chốt
int right = high - 1; // Phần tử thứ 2 từ bên phải mảng
int left = low; // left là phần tử đầu tiên của mảng
while (true)
{
// Trong khi a[left] nhỏ hơn pivot, tăng left
while (a[left] < pivot && left <= right) left++;
// Trong khi a[right] > pivot, giảm right
while (a[right] > pivot && right >= left) right--;
// Sau 2 vòng lặp white, a[left] > pivot và a[right] < pivot
if (left >= right) // Nếu left vượt quá right, dừng
break;
swap(a[left], a[right]); // Đổi chỗ cho phần tử nhỏ hơn về trái, lớn hơn về phải pivot
left++; // Xét tới left, right tiếp theo
right--;
}
swap(a[left], a[high]); // Đổi chỗ pivot về giữa mảng
quickSort(a, low, left - 1); // Đệ quy mảng bên trái
quickSort(a, left + 1, high); // Đệ quy mảng bên phải
}
}
4. Đánh giá thuật toán sắp xếp nhanh
Bạn cần quan tâm một điều đó là “ sắp xếp nhanh ” chỉ là tên của thuật toán, không có nghĩa nó nhanh hơn trọn vẹn so với những thuật toán khác. Tùy từng trường hợp vận tốc thuật toán sẽ khác nhau. Bạn hoàn toàn có thể tìm hiều thêm những thuật toán sắp xếp khác tại đây
Bảng đánh giá độ phức tạp của thuật toán:
| Trường hợp | Độ phức tạp | Bộ nhớ sử dụng |
| Tốt nhất | O (n log n) | log n |
| Trung bình | O (n log n) | log n |
| Xấu nhất | O(n^2 ) | log n |
Trường hợp xấu nhất xảy ra khi mỗi lần phân đoạn, ta chọn phải thành phần lớn nhất hoặc nhỏ nhất làm chốt .
Trường hợp tốt nhất khi mỗi lần phân đoạn, hai mảng con có độ dài bằng nhau .
Ưu điểm:
- Thuật toán có độ phức tạp nhỏ hơn các thuật toán sắp xếp đơn giản, tốc độ xử lý tương đối nhanh. Trong một số trường hợp, quicksort là thuật toán có tốc độ tốt nhất
- Thông dụng, được áp dụng nhiều trong lập trình, trong thư viện của các ngôn ngữ lập trình như C++, Java, C#. . .
- Có thể ứng dụng vào xử lý dữ liệu lớn
Nhược điểm:
- Thuật toán không có tính ổn định, không có tính thích ứng, dễ ảnh hưởng bởi dữ liệu đầu vào
- Tốn không gian bộ nhớ hơn so với các thuật toán sắp xếp đơn giản
- Tư tưởng và giải thuật khá phức tạp
- Khó khăn trong việc lựa chọn phần tử làm chốt trong phân hoạch. Việc lựa chọn có thể ảnh hưởng rất nhiều đến hiệu suất của thuật toán tuy nhiên ta không thế đưa ra lựa chọn tối ưu nhất.
Lời kết
Trên đây là toàn bộ nội dung về Quick Sort mong giúp bạn có thể làm chủ được nó. Các kiến thức, nội dung do mình tổng hợp và sưu tầm tử nhiều nguồn khác nhau.
Nếu có thể, xem thêm các các thuật toán quan trọng với lập trình viên tại đây.
Cuối cùng, mình gửi lời cảm ơn tới bạn đọc đã đọc tới dòng này của mình. Chúc bạn thành công xuất sắc !
Source: https://final-blade.com
Category: Kiến thức Internet