Thuật toán Selection Sort - Giới thiệu chi tiết và code ví dụ trên nhiều ngôn ngữ lập trình » https://final-blade.com

Chào ace, bài này chúng ta sẽ tìm hiểu về một trong các thuật toán sắp xếp được sử dụng nhiều trong lập trình và thực tế nhất đó là Selection Sort, sau đây cafedev sẽ giới thiệu và chia sẻ chi tiết(khái niệm, ứng dụng của nó, code ví dụ, điểm mạnh, điểm yếu…) về Selection Sort thông qua các phần sau.

Tóm Tắt

1. Giới thiệu

Thuật toán sắp xếp lựa chọn(Selection Sort) sắp xếp một mảng bằng cách liên tục tìm phần tử tối thiểu (xét theo thứ tự tăng dần) từ phần không được sắp xếp và đặt nó ở đầu. Thuật toán duy trì hai mảng con trong một mảng nhất định.

Bạn đang đọc: Thuật toán Selection Sort – Giới thiệu chi tiết và code ví dụ trên nhiều ngôn ngữ lập trình » https://final-blade.com

1 ) Mảng con đã được sắp xếp .
2 ) Mảng con còn lại chưa được sắp xếp .
Trong mỗi lần lặp lại sắp xếp lựa chọn, thành phần tối thiểu ( xét theo thứ tự tăng dần ) từ mảng con chưa được sắp xếp được chọn và chuyển đến mảng con đã sắp xếp .
Ví dụ sau lý giải những bước trên :

arr [] = 64 25 12 22 11

// Tìm phần tử nhỏ nhất trong arr [0 ... 4]
// và đặt nó ở đầu
11 25 12 22 64

// Tìm phần tử nhỏ nhất trong arr [1 ... 4]
// và đặt nó ở đầu arr [1 ... 4]
11 12 25 22 64

// Tìm phần tử nhỏ nhất trong arr [2 ... 4]
// và đặt nó ở đầu arr [2 ... 4]
11 12 22 25 64

// Tìm phần tử nhỏ nhất trong arr [3 ... 4]
// và đặt nó ở đầu arr [3 ... 4]
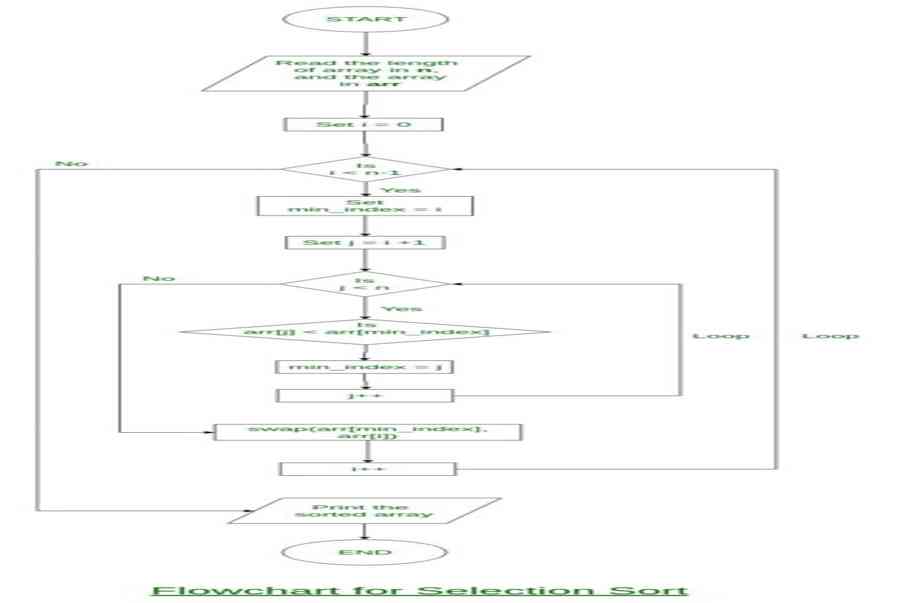
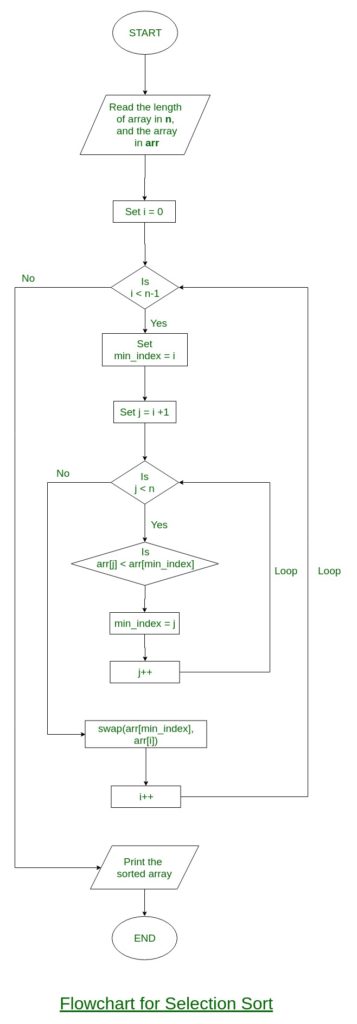
11 12 22 25 64

Hình ảnh luồng giải quyết và xử lý của Selection sort :

2. Code ví dụ trên nhiều ngôn từ lập trình

C++

// C++ program for implementation of selection sort  
#include  
using namespace std; 
  
void swap(int *xp, int *yp)  
{  
    int temp = *xp;  
    *xp = *yp;  
    *yp = temp;  
}  
  
void selectionSort(int arr[], int n)  
{  
    int i, j, min_idx;  
  
    // One by one move boundary of unsorted subarray  
    for (i = 0; i < n-1; i++)  
    {  
        // Find the minimum element in unsorted array  
        min_idx = i;  
        for (j = i+1; j < n; j++)  
        if (arr[j] < arr[min_idx])  
            min_idx = j;  
  
        // Swap the found minimum element with the first element  
        swap(&arr[min_idx], &arr[i]);  
    }  
}  
  
/* Function to print an array */
void printArray(int arr[], int size)  
{  
    int i;  
    for (i=0; i < size; i++)  
        cout << arr[i] << " ";  
    cout << endl;  
}  
  
// Driver program to test above functions  
int main()  
{  
    int arr[] = {64, 25, 12, 22, 11};  
    int n = sizeof(arr)/sizeof(arr[0]);  
    selectionSort(arr, n);  
    cout << "Sorted array: \n";  
    printArray(arr, n);  
    return 0;  
}


// C program for implementation of selection sort 
#include  
  
void swap(int *xp, int *yp) 
{ 
    int temp = *xp; 
    *xp = *yp; 
    *yp = temp; 
} 
  
void selectionSort(int arr[], int n) 
{ 
    int i, j, min_idx; 
  
    // One by one move boundary of unsorted subarray 
    for (i = 0; i < n-1; i++) 
    { 
        // Find the minimum element in unsorted array 
        min_idx = i; 
        for (j = i+1; j < n; j++) 
          if (arr[j] < arr[min_idx]) 
            min_idx = j; 
  
        // Swap the found minimum element with the first element 
        swap(&arr[min_idx], &arr[i]); 
    } 
} 
  
/* Function to print an array */
void printArray(int arr[], int size) 
{ 
    int i; 
    for (i=0; i < size; i++) 
        printf("%d ", arr[i]); 
    printf("\n"); 
} 
  
// Driver program to test above functions 
int main() 
{ 
    int arr[] = {64, 25, 12, 22, 11}; 
    int n = sizeof(arr)/sizeof(arr[0]); 
    selectionSort(arr, n); 
    printf("Sorted array: \n"); 
    printArray(arr, n); 
    return 0; 
}

Python


# Python program for implementation of Selection 
# Sort 
import sys 
A = [64, 25, 12, 22, 11] 
  
# Traverse through all array elements 
for i in range(len(A)): 
      
    # Find the minimum element in remaining  
    # unsorted array 
    min_idx = i 
    for j in range(i+1, len(A)): 
        if A[min_idx] > A[j]: 
            min_idx = j 
              
    # Swap the found minimum element with  
    # the first element         
    A[i], A[min_idx] = A[min_idx], A[i] 
  
# Driver code to test above 
print ("Sorted array") 
for i in range(len(A)): 
    print("%d" %A[i]),

Java

// Java program for implementation of Selection Sort 
class SelectionSort 
{ 
    void sort(int arr[]) 
    { 
        int n = arr.length; 
  
        // One by one move boundary of unsorted subarray 
        for (int i = 0; i < n-1; i++) 
        { 
            // Find the minimum element in unsorted array 
            int min_idx = i; 
            for (int j = i+1; j < n; j++) 
                if (arr[j] < arr[min_idx]) 
                    min_idx = j; 
  
            // Swap the found minimum element with the first 
            // element 
            int temp = arr[min_idx]; 
            arr[min_idx] = arr[i]; 
            arr[i] = temp; 
        } 
    } 
  
    // Prints the array 
    void printArray(int arr[]) 
    { 
        int n = arr.length; 
        for (int i=0; i

Xem thêm: Vòng lặp for trong C++ (có bài tập thực hành)

// C# program for implementation  
// of Selection Sort 
using System; 
  
class GFG 
{  
    static void sort(int []arr) 
    { 
        int n = arr.Length; 
  
        // One by one move boundary of unsorted subarray 
        for (int i = 0; i < n - 1; i++) 
        { 
            // Find the minimum element in unsorted array 
            int min_idx = i; 
            for (int j = i + 1; j < n; j++) 
                if (arr[j] < arr[min_idx]) 
                    min_idx = j; 
  
            // Swap the found minimum element with the first 
            // element 
            int temp = arr[min_idx]; 
            arr[min_idx] = arr[i]; 
            arr[i] = temp; 
        } 
    } 
  
    // Prints the array 
    static void printArray(int []arr) 
    { 
        int n = arr.Length; 
        for (int i=0; i

PHP


 $arr[$low]) 
        { 
            $tmp = $arr[$i]; 
            $arr[$i] = $arr[$low]; 
            $arr[$low] = $tmp; 
        } 
    } 
} 
  
// Driver Code 
$arr = array(64, 25, 12, 22, 11); 
$len = count($arr); 
selection_sort($arr, $len); 
echo "Sorted array : \n";  
  
for ($i = 0; $i < $len; $i++)  
    echo $arr[$i]. " ";  
  
// This code is contributed  
// by Deepika Gupta.  
?>

Kết quả :

Sorted array: 
11 12 22 25 64

3. Độ phức tạp

Độ phức tạp thời gian: O (n2) vì có hai vòng lặp lồng nhau.

Không gian phụ trợ: O (1)

Điều tốt về sắp xếp lựa chọn là nó không khi nào tạo ra nhiều hơn O ( n ) hoán đổi và hoàn toàn có thể có ích khi ghi bộ nhớ là một hoạt động giải trí tốn kém .

4. Bài tập

Sắp xếp một mảng chuỗi bằng cách dùng Selection Sort

Bài giải

Nguồn và Tài liệu tiếng anh tham khảo:

Tài liệu từ cafedev:

Nếu bạn thấy hay và hữu dụng, bạn hoàn toàn có thể tham gia những kênh sau của cafedev để nhận được nhiều hơn nữa :
Chào thân ái và quyết thắng !

Xem thêm: Các kiểu dữ liệu trong C++ và cách khai báo

Đăng ký kênh youtube để ủng hộ Cafedev nha các bạn, Thanks you!

Source: https://final-blade.com
Category: Kiến thức Internet

admin

final-blade.com