Các bạn đã chán với thuật toán chưa? Học thuật toán hay mà ^^. Nối tiếp series thuật toán chuyên sâu này, chúng ta sẽ tiếp tục thảo luận về một thuật toán vô cùng phổ biến, nghe tên là bạn thấy quen liền. Đó là thuật toán tìm kiếm nhị phân hay Binary Search Tree.
Chúng ta sẽ triển khai các chức năng của thuật toán để tìm kiếm, chèn và xóa các giá trị từ một cây nhị phân. Vẫn là hai phương pháp để bạn tiếp cận và thực hiện thuật toán là: sử dụng vòng lặp và đệ quy.
Binary Search Tree (BTS)
Một Binary Search Tree có thuộc tính sau:
- Tất cả các node phải sao cho node con bên trái luôn nhỏ hơn node cha.
- Node con bên phải luôn lớn hơn node cha.
Hình dưới đây là một minh họa cho một cây nhị phân, khi mà dữ liệu được tổ chức giống như một cây.
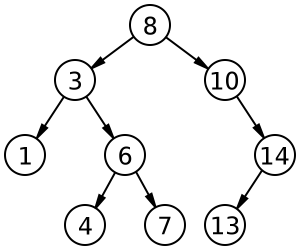
Trong các phần sau, chúng ta sẽ xem cách tìm kiếm, chèn và xóa trong BTS bằng cả hai phương pháp: sử dụng vòng lặp và đệ quy.
🔥 Đọc thêm về thuật toán:
Trước tiên, hãy tạo cấu trúc dữ liệu Binary Search Tree:
public class BinaryTree {
public TreeNode root;
public static class TreeNode {
public TreeNode left;
public TreeNode right;
public Object data;
public TreeNode(Object data) {
this.data = data;
left = right = null;
}
}
}
Tìm kiếm đệ quy BST
Đoạn code dưới đây sẽ thực thi việc tìm kiếm một giá trị trong tree theo phương pháp đệ quy.
public class SearchInsertRemoveFromTree {
public static void main(String[] args) {
/**
* Our Example Binary Search Tree
* 10
* 5 20
* 4 8 15 25
*/
BinaryTree tree = new BinaryTree();
tree.root = new TreeNode(10);
tree.root.left = new TreeNode(5);
tree.root.right = new TreeNode(20);
tree.root.left.left = new TreeNode(4);
tree.root.left.right = new TreeNode(8);
tree.root.right.left = new TreeNode(15);
tree.root.right.right = new TreeNode(25);
System.out.println("Search Value 2 is in tree? " + searchRecursively(tree.root, 2));
System.out.println("Search Value 10 in tree? " + searchRecursively(tree.root, 10));
}
public static boolean searchRecursively(TreeNode root, int value) {
if (root == null)
return false;
if ((int) root.data == value)
return true;
if (value < (int) root.data)
return searchRecursively(root.left, value);
else if (value > (int) root.data)
return searchRecursively(root.right, value);
return false;
}
}
Kết quả thu được:
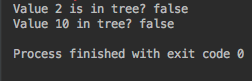
Tìm kiếm nhị phân BST sử dụng vòng lặp
Vẫn với yêu cầu tìm kiếm tương tự như phần trên, nhưng lần này chúng ta sử dụng phương pháp dùng vòng lặp.
Với phương pháp dùng vòng lặp, nó có ưu điểm là dễ debug hơn nhiều so với đệ quy.
public static boolean searchIteratively(TreeNode root, int value) {
while (root != null) {
if ((int) root.data == value)
return true;
if (value < (int) root.data)
root = root.left;
else
root = root.right;
}
return false;
}
Chèn thêm một giá trị vào cây nhị phân bằng đệ quy
public static TreeNode insertionRecursive(TreeNode root, int value) {
if (root == null)
return new TreeNode(value);
if (value < (int) root.data) {
root.left = insertionRecursive(root.left, value);
} else if (value > (int) root.data) {
root.right = insertionRecursive(root.right, value);
}
return root;
}
public static void printInorderTraversal(TreeNode root) {
if (root != null) {
printInorderTraversal(root.left);
System.out.print(root.data + " ");
printInorderTraversal(root.right);
}
}
Giả sử chúng ta gọi hàm trên trong main(), bạn làm như sau:
tree.root = insertionRecursive(tree.root, 24); tree.root = insertionRecursive(tree.root, 2); printInorderTraversal(tree.root);
Cây được in dưới dạng inorder traversal
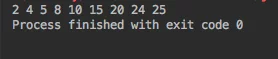
Chèn thêm một giá trị vào cây nhị phân bằng vòng lặp
Để làm được điều này trong cây BST, chúng ta sẽ cần duyệt qua cây bằng cách sử dụng hai con trỏ.
public static TreeNode insertionIterative(TreeNode root, int value) {
TreeNode current, parent;
TreeNode tempNode = new TreeNode(value);
if (root == null) {
root = tempNode;
return root;
} else {
current = root;
}
while (true) {
parent = current;
if (value < (int) current.data) {
current = current.left;
if (current == null) {
parent.left = tempNode;
return root;
}
} else if (value > (int) current.data) {
current = current.right;
if (current == null) {
parent.right = tempNode;
return root;
}
}
}
}
Xóa một phần tử trong cây nhị phân bằng cách đệ quy
Việc xóa phần tử khỏi cây nhị phân phức tạp hơn so với tìm kiếm và chèn một chút. Vì chúng ta phải đảm bảo rằng hai thuộc tính của cây nhị phân vẫn được bảo toàn.
Để xóa một phần tử, trước tiên chúng ta cần tìm kiếm và xác định được nó đã. Sau đó, chúng ta cần xác định xem phần tử đó có phần tử con hay không!
- Nếu không có con – Chỉ cần xóa.
- Nếu có một con – Sao chép con đó vào node.
- Nếu có hai con – Xác định phần tử cao nhất tiếp theo (con kế nhiệm inorder) trong cây con bên phải. Thay thế node bị xóa bằng node kế nhiệm nhỏ hơn. Xóa bản sao kế nhiệm inorder.
Có thể thu được giá trị kế nhiệm inorder bằng cách tìm giá trị nhỏ nhất trong con bên phải của node.
Chương trình java sau đây xóa các phần tử khỏi BST:
public static TreeNode deleteRecursively(TreeNode root, int value) {
if (root == null)
return root;
if (value < (int) root.data) {
root.left = deleteRecursively(root.left, value);
} else if (value > (int) root.data) {
root.right = deleteRecursively(root.right, value);
} else {
if (root.left == null) {
return root.right;
} else if (root.right == null)
return root.left;
root.data = inOrderSuccessor(root.right);
root.right = deleteRecursively(root.right, (int) root.data);
}
return root;
}
public static int inOrderSuccessor(TreeNode root) {
int minimum = (int) root.data;
while (root.left != null) {
minimum = (int) root.left.data;
root = root.left;
}
return minimum;
}
Giả sử chúng ta gọi hàm trên trong main(), bạn làm như sau:
tree.root = deleteRecursively(tree.root, 4); tree.root = deleteRecursively(tree.root, 20); printInorderTraversal(tree.root);
Đầu ra là:
2 5 8 10 15 24 25
Hãy làm tương tự lặp đi lặp lại.
Xóa một phần tử trong cây nhị phân bằng cách sử dụng vòng lặp
public static TreeNode deleteNodeIteratively(TreeNode root, int value) {
TreeNode parent = null, current = root;
boolean hasLeft = false;
if (root == null)
return root;
while (current != null) {
if ((int) current.data == value) {
break;
}
parent = current;
if (value < (int) current.data) {
hasLeft = true;
current = current.left;
} else {
hasLeft = false;
current = current.right;
}
}
if (parent == null) {
return deleteNodeIteratively(current);
}
if (hasLeft) {
parent.left = deleteNodeIteratively(current);
} else {
parent.right = deleteNodeIteratively(current);
}
return root;
}
private static TreeNode deleteNodeIteratively(TreeNode node) {
if (node != null) {
if (node.left == null && node.right == null) {
return null;
}
if (node.left != null && node.right != null) {
TreeNode inOrderSuccessor = deleteInOrderSuccessorDuplicate(node);
node.data = inOrderSuccessor.data;
} else if (node.left != null) {
node = node.left;
} else {
node = node.right;
}
}
return node;
}
private static TreeNode deleteInOrderSuccessorDuplicate(TreeNode node) {
TreeNode parent = node;
node = node.right;
boolean rightChild = node.left == null;
while (node.left != null) {
parent = node;
node = node.left;
}
if (rightChild) {
parent.right = node.right;
} else {
parent.left = node.right;
}
node.right = null;
return node;
}
Độ phức tạp của thuật toán BST là 0(h). Trong đó h là độ cao của cây.
Bài viết của mình đến đây là hết rồi. Mình hi vọng vẫn cảm thấy thích thú với thuật toán ^^
Nguồn tham khảo:
- https://en.wikipedia.org/wiki/Binary_search_tree
- https://www.cs.usfca.edu/~galles/visualization/BST.html
- https://www.journaldev.com/23086/binary-search-tree-bst-search-insert-remove