Chương 4: Câu lệnh điều kiện và đệ quy Java

Trở về Mục lục cuốn sách

Tóm Tắt

4.1 Toán tử chia dư

Toán tử chia dư tính với các số nguyên (cùng các biểu thức số nguyên) và cho kết quả là phần dư của phép chia số thứ nhất cho số thứ hai. Trong Java, toán tử chia dư có kí hiệu là dấu phần trăm, %. Cú pháp cũng giống như các toán tử khác:

    int
Bạn đang đọc: Chương 4: Câu lệnh điều kiện và đệ quy Java 
 quotient = 7 / 3; int remainder = 7 % 3;

Với toán tử thứ nhất, chia nguyên, tác dụng là 2. Với toán tử thứ hai ta được hiệu quả bằng 1. Như vậy 7 chia cho 3 bằng 2 dư 1 .

Toán tử số dư bất ngờ trở nên có ích. Chẳng hạn, bạn có thể kiểm tra xem một số có chia hết cho số khác không: nếu x % y bằng không thì x chia hết cho y.

Hơn nữa, bạn còn có thể lọc ra những chữ số cuối cùng bên phải từ số ban đầu. Chẳng hạn, x % 10 cho ta số hàng đơn vị của x (trong hệ thập phân). Tương tự, x % 100 cho ta hai chữ số hàng chục và đơn vị.

4.2 Thực hiện lệnh theo điều kiện

Để viết được những chương trình hữu ích, chúng ta thường luôn phải kiểm tra những điều kiện và thay đổi biểu hiện tương ứng của chương trình. Các câu lệnh điều kiện cung cấp cho ta khả năng này. Dạng đơn giản nhất là lệnh if:

if (x > 0) { 
    System.out.println(" x la so duong "); 
  }

Biểu thức ở trong cặp ngoặc tròn được gọi là điều kiện kèm theo. Nếu nó được thoả mãn thì đoạn lệnh bên trong cặp ngoặc nhọn được thực thi. Nếu không, sẽ chẳng có điều gì xảy ra .

Điều kiện có thể chứa bất kì toán tử so sánh nào, vốn đôi khi còn được gọi là toán tử quan hệ:

  x == y / / x bằng y 
  x != y / / x không bằng y 
  x > y / / x is lớn hơn y 
  x < y / / x nhỏ hơn y  x >= y / / x lớn hơn hoặc bằng y 
  x <= y / / x nhỏ hơn hoặc bằng y

Mặc dù có thể bạn đã quen thuộc với những phép toán này, cú pháp dùng trong Java vẫn hơi khác những biểu thức như =, ≠ và ≤. Một lỗi thường mắc phải là dùng một dấu = thay vì hai ==. Hãy nhớ rằng = là toán tử gán, còn == là toán tử so sánh. Ngoài ra không có toán tử nào được viết là =< hoặc =>.

Hai vế trong một biểu thức điều kiện phải có cùng kiểu dữ liệu. Bạn chỉ được phép so sánh int với ints hoặc double với double.

Hai toán tử == và != cũng làm việc với các chuỗi kí tự, nhưng cách hoạt động của chúng không giống như bạn đã dự kiến. Còn tất cả những toán tử quan hệ khác thì không có tác dụng gì đối với chuỗi. Ta sẽ xem cách so sánh chuỗi ở Mục 8.10.

4.3 Thực hiện chọn lựa

Dạng thứ hai của thực thi teho điều kiện kèm theo là triển khai lệnh theo lựa chọn, trong đó có hai năng lực và điều kiện kèm theo được đặt ra để địa thế căn cứ vào đó mà lựa chọn triển khai một trong hai. Cú pháp có dạng như sau :

if (x%2 == 0) { 
      System.out.println(" x la so chan "); 
    } else { 
      System.out.println(" x la so le "); 
    }

Nếu phần dư của phép chia x cho 2 là 0, thì chúng ta biết rằng x là số chẵn, và chương trình sẽ hiển thị thông báo điều này. Nếu điều kiện không được thoả mã thì lệnh thứ hai sẽ được thực hiện. Vì điều kiện hoặc là được thoả mãn, hoặc không; nên luôn chỉ có một trong hai phương án được thực hiện.

Nhân tiện nói thêm, nếu bạn có dự tính tiếp tục kiểm tra tính chẵn lẻ, hoàn toàn có thể bạn sẽ muốn “ gói ” đoạn mã lệnh này vào trong một phương pháp, như sau :

public static void printParity(int x) { 
if (x%2 == 0) { 
      System.out.println(" x la so chan "); 
    } else { 
      System.out.println(" x la so le "); 
    } 
  }

Bây giờ bạn có một phương thức tên là printParity để in ra thông báo thích hợp cho mỗi số nguyên bạn cung cấp cho nó. Trong main bạn sẽ kích hoạt phương thức này như sau:

    printParity(17);

Hãy luôn nhớ rằng khi bạn kích hoạt một phương pháp, thì không nhất thiết phải khai báo những kiểu của đối số được cung ứng. Java hoàn toàn có thể tưởng tượng ra kiểu tài liệu là gì. Bạn phải kiềm chế để tránh viết những lệnh kiểu như :

int number = 17; 
    printParity(int number); / / SAI ! ! !

4.4 Các điều kiện xâu chuỗi

Đôi khi bạn cần phải kiểm tra một số các điều kiện có liên quan và chọn trong một số những hành động. Một cách thực hiện việc này là xâu chuỗi một loạt các if và else:

if (x > 0) { 
      System.out.println(" x la so duong "); 
    } else if (x < 0) { 
      System.out.println(" x la so am "); 
    } else { 
      System.out.println(" x bang khong "); 
    }

Việc xâu chuỗi như vậy hoàn toàn có thể dài tùy ý, mặc dầu chúng hoàn toàn có thể khó đọc nếu đi quá đà. Một cách làm để dễ đọc hơn là sử dụng quy tắc thụt đầu dòng tiêu chuẩn, như đã trình diễn trong những ví dụ trên. nếu bạn giữ cho những câu lệnh và những ngoặc nhọn được thẳng hàng với nhua thì ít có năng lực gây lỗi cú pháp hơn, và nếu có thì cũng dễ tìm thấy hơn .

4.5 Các điều kiện lồng ghép

Ngoài việc xâu chuỗi, bạn còn hoàn toàn có thể lồng ghép một điều kiện kèm theo bên trong điều kiện kèm theo khác. Ta hoàn toàn có thể viết lại ví dụ trên như sau :

if (x == 0) { 
      System.out.println(" x bang khong "); 
    } else { 
if (x > 0) { 
        System.out.println(" x la so duong "); 
      } else { 
        System.out.println(" x la so am "); 
      } 
    }

Bây giờ thì câu lệnh điều kiện bên ngoài có hai nhánh. Nhánh thứ nhất chỉ chứa một lệnh print, nhánh thứ hai lại chứa một câu lệnh điều kiện khác, mà bản thân nó lại có hai nhánh. Hai nhánh này đều chứa những câu lệnh print đơn giản, mặc dù dĩ nhiên chúng có thể là những câu lệnh điều kiện khác.

Tuy cách viết thụt vào trong làm cho cấu trúc rõ ý, nhưng những lệnh điều kiện kèm theo lồng ghép trở nên rất khó để người đọc nhanh. Ta nên nỗ lực tránh dùng chúng .

Mặt khác, dạng cấu trúc lồng ghép này cũng thường thấy, và sau này ta còn gặp chúng, do vậy bạn cũng làm quen với nó.

4.6 Câu lệnh return

Câu lệnh return cho phép bạn kết thúc việc thực thi của một phương thức trước khi đến cuối phương thức đó. Một lí do dùng câu lệnh này là nếu bạn phát hiện ra điều kiện gây lỗi:

public static void printLogarithm(double x) { 
if (x <= 0.0) { 
      System.out.println(" Yêu cau nhap vao so duong. "); 
return; 
    } 
double result = Math.log(x); 
    System.out.println(" Gia tri log cua x bang " + result); 
  }

Mã lệnh này định nghĩa một phương thức có tên printLogarithm; nó nhận tham số là một double có tên x. Phương thức này kiểm tra xem liệu x có nhỏ hơn hoặc bằng 0 hay không, và trong trường hợp như vậy thì in ra một thông báo lỗi rồi dùng return để thoát khỏi phương thức. Luồng thực thi sẽ lập tức trở lại chỗ gọi phương thức đó và những dòng còn lại của phương thức sẽ không được thực hiện.

Tôi đã dùng một giá trị dấu phẩy động ở bên vế phải của điều kiện kèm theo vì vế trái biểu thức này là một biến phẩy động .

4.7 Chuyển đổi kiểu

Bạn có thể tự hỏi rằng làm sao chương trình của ta có thể êm xuôi với biểu thức kiểu như "Gia tri log cua x bang " + result, bởi một toán hạng là String còn toán hạng kia là double. Truong trường hợp này Java đã thông minh để thay ta chuyển giá trị double thành String trước khi thực hiện việc ghép chuỗi.

Mỗi khi bạn thử “cộng” hai biểu thức, mà một trong số đó là String, Java sẽ chuyển đổi cái còn lại thành String rồi mới thực hiện ghép chuỗi. Bạn nghĩ điều gì sẽ xảy ra nếu thực hiện phép cộng giữa một số nguyên với một giá trị phẩy động?

4.8 Đệ quy

Ở chương trước tôi đã nói rằng việc một phương pháp kích hoạt phương pháp khác là hợp lệ, và a đã xét vài ví dụ. Tôi chưa đề cập rằng một phương pháp kích hoạt chính nó cũng hợp lệ. Mặc dù hình thức bề ngoài thì hoàn toàn có thể điều này không rõ hay dở ra làm sao, nhưng thực ra đó chính là một trong những đặc thù hay nhất trong lập trình .
Chẳng hạn, hãy xét phương pháp sau :

public static void countdown(int n) { 
if (n == 0) { 
      System.out.println(" Bum ! "); 
    } else { 
      System.out.println(n); 
      countdown(n-1); 
    } 
  }

Phương thức có tên là countdown và nó nhận tham số là một số nguyên. Nếu tham số bằng 0 hoặc âm, chương trình sẽ in ra chữ, “Bùm!” Còn nếu không, nó sẽ in ra giá trị tham số và sau đó kích hoạt một phương thức có tên countdown—nghĩa là chính nó—nhưng truyền vào đối số n-1.

Điều gì sẽ xảy ra khi ta kích hoạt một phương thức kiểu như thế này?

Xem thêm: Cách CRACK OFFICE 2010 cực kỳ đơn giản ai cũng có thể làm được

  countdown(3);

Việc thực hiện countdown bắt đầu với n=3, và do n lớn hơn 0, nó đưa ra giá trị 3, và rồi gọi chính nó…

Việc thực hiện countdown bắt đầu với n=2, và do n lớn hơn 0, nó đưa ra giá trị 2, và rồi gọi chính nó…

Việc thực hiện countdown bắt đầu với n=1, và do n lớn hơn 0, nó đưa ra giá trị 1, và rồi gọi chính nó…

Việc thực hiện countdown bắt đầu với n=0, và do n không còn lớn hơn 0, nó đưa ra dòng chữ “Bùm!” và rồi quay về.

Phương thức countdown ứng với n=1 quay về.

Phương thức countdown ứng với n=2 quay về.

Phương thức countdown ứng với n=3 quay về.

Và rồi bạn trở về với main. Như vậy, toàn bộ kết quả đầu ra như sau:

3
2
1
Bum!

Ví dụ thứ hai là hãy xem lại các phương thức newLine và threeLine.

public static void newLine() { 
    System.out.println(" "); 
  } 
public static void threeLine() { 
    newLine(); newLine(); newLine(); 
  }

Mặc dù cách này có tính năng, nhưng sẽ không giúp ích được nhiều trong trường hợp ta cần in 2, hoặc 106 dòng mới. Một cách làm hay hơn là

public static void nLines(int n) { 
if (n > 0) { 
      System.out.println(" "); 
      nLines(n-1); 
    } 
  }

Chương trình này tương tự như countdown; khi n còn lớn hơn 0, nó sẽ in ra một dòng mới và sau đó sẽ kích hoạt chính nó để in thêm n - 1 dòng mới nữa. Như vậy số dòng kết quả sẽ là 1 + (n-1), tức là bằng n.

Khi một phương thức kích hoạt chính nó, điều này gọi là đệ quy, và những phương thức đó có tính đệ quy.

4.9 Biểu đồ ngăn xếp cho các phương thức đệ quy

Trong chương trước, tất cả chúng ta đã dùng một biểu đồ ngăn xếp để bộc lộ trạng thái của một chương trình trong quy trình phương pháp được kích hoạt. Loại biểu đồ này cũng tiện dùng cho việc diễn giải một phương pháp đệ quy .
Hãy nhơ rằng mỗi khi phương pháp được kích hoạt, Java tạo ra một “ khung ” mới trong đó có chứa phiên bản mới của những biến cục bộ và tham số trong phương pháp .

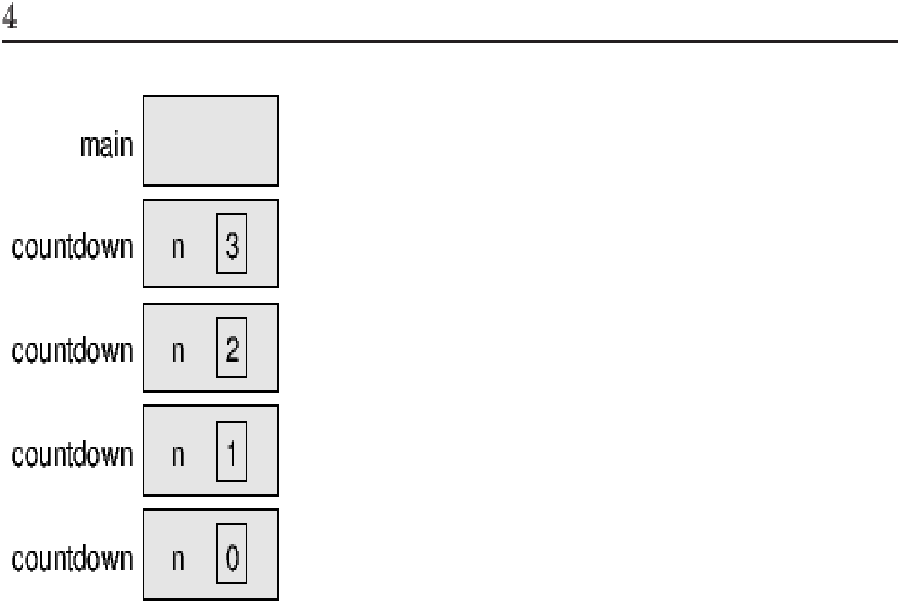
Hình vẽ này minh hoạ một sơ đồ ngăn xếp cho phương thức countdown khi gọi với n = 3:

Có một khung dành cho main và bốn khung countdown, mỗi khung có một giá trị riêng cho tham biến n. Đáy của ngăn xếp, countdown với n=0, được gọi là trường hợp cơ sở. Nó không thực hiện lời gọi đệ quy, do đó không có thêm khung countdown nào.

Khung chứa main thì rỗng vì main không chứa bất kì tham số hay biến nào.

4.10 Thuật ngữ

toán tử module:: Toán tử dùng với hai số nguyên và trả lại phần dư trong phép chia giữa hai số đó. Trong Java, toán tử này được kí hiệu bởi dấu phần trăm (%).
lệnh điều kiện:: Một khối lệnh có thể được thực thi hay không tùy theo một điều kiện nào đó.
xâu chuỗi:: Cách nối nhiều lệnh điều kiện thành dãy liên tục.
lồng ghép:: Cách đặt một lệnh điều kiện này vò trong một hoặc cả hai nhánh của một lệnh điều kiện khác.
định kiểu:: Một toán tử giúp chuyển đổi từ kiểu dữ liệu này sang kiểu khác. Trong Java nó có dạng tên một kiểu dữ liệu viết giữa cặp ngoặc tròn, như (int).
đệ quy:: Quá trình kích hoạt chính phương thức đang được thực thi.
trường hợp cơ sở:: Một điều kiện để cho phương thức đệ quy không kích hoạt đệ quy nữa.

4.11 Bài tập

Bài tập 1 Hãy vẽ một biểu đồ ngăn xếp biểu diễn trạng thái chương trình ở Mục main kích hoạt nLines với tham số n=4, ngay trước khi lần kích hoạt cuối cùng của nLines trả về.Hãy vẽ một biểu đồ ngăn xếp trình diễn trạng thái chương trình ở Mục 4.8 sau khikích hoạtvới tham số, ngay trước khi lần kích hoạt ở đầu cuối củatrả về .Bài tập 2 Bài tập này ôn lại luồng thực thi, bằng một chương trình với nhiều phương thức. Hãy đọc mã lệnh dưới đây rồi trả lời những câu hỏi đi theo.

public class Buzz { 

public static void baffle(String blimp) { 
    System.out.println(blimp); 
    zippo(" ping ", -5); 
  } 
public static void zippo(String quince, int flag) { 
if (flag < 0) { 
      System.out.println(quince + " zoop "); 
    } else { 
      System.out.println(" ik "); 
      baffle(quince); 
      System.out.println(" boo-wa-ha-ha "); 
    } 
  } 
public static void main(String[] args) { 
    zippo(" rattle ", 13); 
  } 
}

Hãy viết số 1 kế bên câu lệnh đầu tiên được thực thi của chương trình này. Hãy cẩn thận để tách biệt những thứ thuộc về câu lệnh với những thứ khác.
Viết số 2 kế bệnh câu lệnh thứ hai, và cứ như vậy đến cuối chương trình. Nếu một câu lệnh được thực hiện nhiều lần thì cuối cùng ta có thể sẽ thấy kết quả in ra chứa nhiều con số ghi bên cạnh nó.
Giá trị của tham số blimp khi baffle bị kích hoạt là gì?
Kết quả của chương trình này là gì?

Bài tập này ôn lại luồng thực thi, bằng một chương trình với nhiều phương pháp. Hãy đọc mã lệnh dưới đây rồi vấn đáp những câu hỏi đi theo .Bài tập 3 Câu đầu trong lời bài hát “99 Bottles of Beer” là:

99 bottles of beer on the wall, 99 bottles of beer, ya ’ take one down, ya ’ pass it around, 98 bottles of beer on the wall .

Câu đầu trong lời bài hát “ 99 Bottles of Beer ” là :Những câu tiếp theo cũng như vậy chỉ khác là số chai bia cứ giảm dần đi một, đến câu ở đầu cuối :

No bottles of beer on the wall, no bottles of beer, ya ’ can’t take one down, ya ’ can’t pass it around, ’ cause there are no more bottles of beer on the wall !

Và sau đó thì ở đầu cuối bài hát cũng kết thúc .
Hãy viết chương trình in ra hàng loạt lời bài hát “ 99 Bottles of Beer. ” Chương trình này cần có một phương pháp đệ quy để xử lý phần khó khăn vất vả, nhưng hoàn toàn có thể bạn còn muốn viết thêm những phương pháp phụ trợ việc phân loại những tính năng cơ bản của chương trình .
Trong quy trình tăng trưởng mã lệnh, hãy thử chạy với 1 số ít ít những câu hát, như “ 3 Bottles of Beer. ”
Mục đích của bài tập này là tiếp đón bài toán rồi chia nhỏ nó thành những bài toán con, và giải bài toán con bằng cách viết những phương pháp đơn thuần .
Bài tập 4 Kết quả của chương trình sau đây là gì?

public class Narf { 

public static void zoop(String fred, int bob) { 
    System.out.println(fred); 
if (bob == 5) { 
      ping(" not "); 
    } else { 
      System.out.println(" ! "); 
    } 
  } 

public static void main(String[] args) { 
int bizz = 5; 
int buzz = 2; 
    zoop(" just for ", bizz); 
    clink(2*buzz); 
  } 

public static void clink(int fork) { 
    System.out.print(" It's "); 
    zoop(" breakfast ", fork) ; 
  } 

public static void ping(String strangStrung) { 
    System.out.println(" any " + strangStrung + " more "); 
  } 
}

Kết quả của chương trình sau đây là gì ?Bài tập 5 Định lý cuối cùng của Fermat phát biểu rằng không có các số nguyên a, b, và c nào thoả mãn

an + bn = cn

Định lý sau cuối của Fermat phát biểu rằng không có những số nguyên a, b, và c nào thoả mãn

trừ trường hợp n = 2.Viết một phương thức có tên là check_fermat nhận vào bốn tham số—a, b, c và n—rồi kiểm tra xem có thoả mãn định lý Fermat không. Nếu n lớn hơn 2 và hoá ra an + bn = cn, thì chương trình sẽ in ra “Trời, Fermat đã lầm!” Còn nếu không thì chương trình sẽ in ra, “Không, vẫn không đúng”.

Bạn cần phải giả sử rằng có một phương thức tên là raiseToPow ; phương thức này nhận đối số là hai số nguyên rồi nâng đối số thứ nhất lên lũy thừa số thứ hai. Chẳng hạn: