Thuật toán sắp xếp vun đống Heap sort trong lập trình, cài đặt thuật toán Heap sort code C/C++. Tìm hiểu về cấu trúc heap, độ phức tạp, ưu nhược điểm heapsort. Cùng tìm hiểu mọi nội dung quanh bài viết nhé!
Tóm Tắt
1. Sắp xếp vun đống
Sắp xếp vun đống – heap sort là một thuật toán sắp xếp nhanh sử dụng kĩ thuật phân loại dựa trên cấu trúc cây nhị phân đặc biệt gọi là đống nhị phân (binary heap). Thuật toán dựa vào sự đặc biệt của cây nhị phân để lựa chọn ra phần tử lớn nhất rồi lần lượt chèn phần tử này vào vùng sắp xếp.
Trong khoa học máy tính các nhà khoa học coi đây là dạng cải tiến của thuật toán sắp xếp Selection sort vì nó cũng sử dụng tư tưởng chọn. Cách chọn của thuật toán được cài tiến và tối ưu nhờ đó hiệu suất của nó tốt hơn selection sort rất nhiều. Heap sort Là một trong các thuật toán sắp xếp thông dụng nhất. Nó mạnh từ tư duy thuật toán cho tới hiệu quả mà nó mang lại, khi gặp các tình huống bạn cần phải sử dụng tới nó, bạn sẽ nhận ra điều này.
Bạn đang đọc: Thuật toán sắp xếp vun đống – Heap Sort Algorithm C/C++
Xem thêm các thuật toán sắp xếp thông dụng khác tại đây
Cấu trúc dữ liệu heap
Cấu trúc đống nhị phân – binary heap hay người ta còn gọi là đống hoặc heap là trái tim của thuật toán. Cấu trúc này là một dạng đặc biệt của cây nhị phân hoàn chỉnh trong đó node con được so sánh với node cha và được sắp xếp một cách phù hợp.
(Cây nhị phân hoàn chỉnh là cây có đầy đủ con ngoại trừ các node cuối).
Heap có 2 dạng heap dựa vào cách so sánh khóa của node con với node cha .
- Max heap khóa của node cha luôn lớn hơn node node con
- Min heap khóa của node cha luôn nhỏ hơn node con
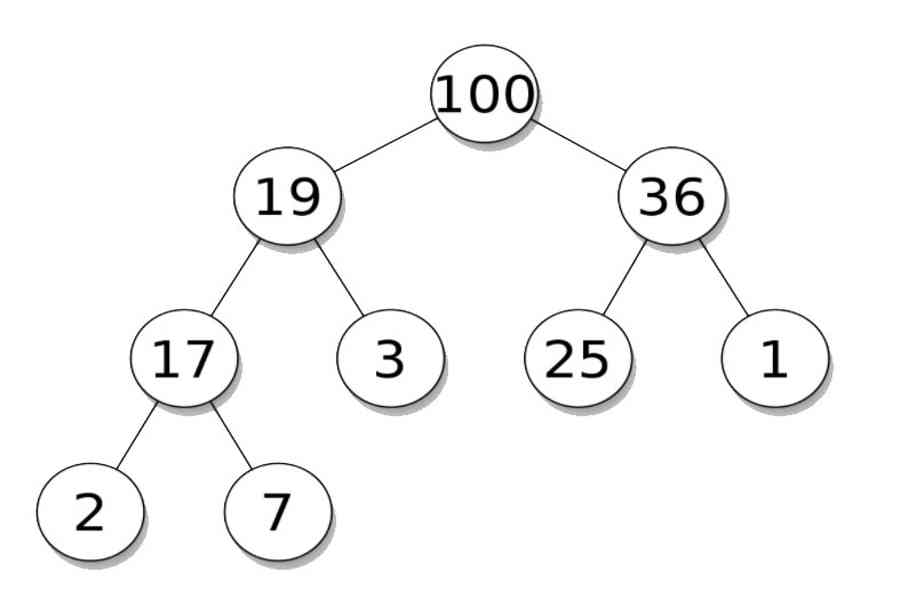
Hình minh họa max heap :
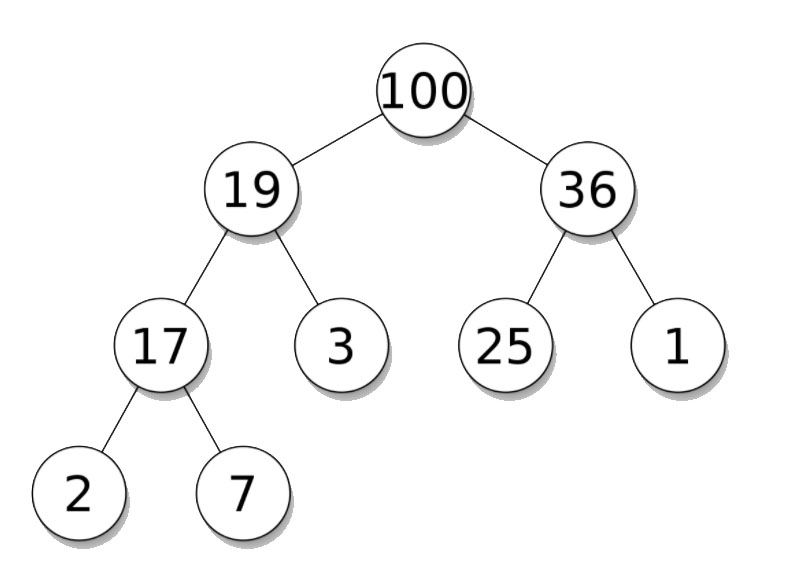 Max heapHình minh họa min heap
Max heapHình minh họa min heap
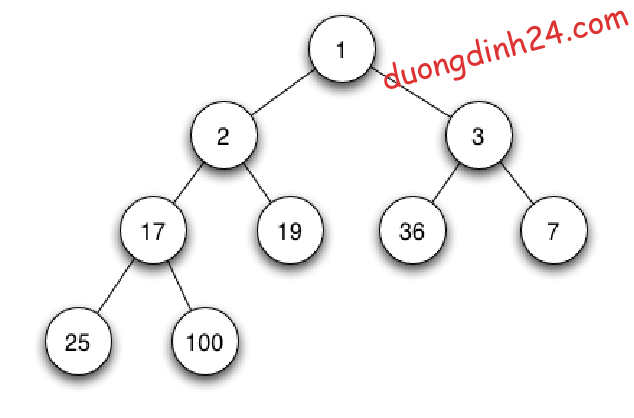 Min heapNếu sắp xếp tăng dần người ta sử dụng max heap, giảm dần sẽ sử dụng min heap. Bài viết này mình sẽ dùng max heap để sắp xếp tăng dần .
Min heapNếu sắp xếp tăng dần người ta sử dụng max heap, giảm dần sẽ sử dụng min heap. Bài viết này mình sẽ dùng max heap để sắp xếp tăng dần .
2. Ý tưởng thuật toán Heap Sort
Thuật toán Heap sort lấy ý tưởng sáng tạo xử lý từ cấu trúc heap, đơn cử :
- Ta coi dãy cần sắp xếp là một cây nhị phân hoàn chỉnh, sau đó hiệu chỉnh cây thành dạng cấu trúc heap ( vun đống)
- Dựa vào tính chất của cấu trúc heap, ta có thể lấy được ra phần từ lớn nhất hoặc nhỏ nhất của dãy, phần tử này chính là gốc của heap. Giảm số lượng phần tử của cây nhị phân và tái cấu trúc heap.
- Đưa phần tử đỉnh heap về đúng vị trí của dãy ở cuối mảng, sau đó giảm số lượng phần tử của mảng (không xét tới phần tử cuối nữa)
- Tái cấu trúc heap và lặp lại việc lấy phần tử gốc của cấu trúc heap cho tới khi danh sách ban đầu chỉ còn 1 phần tử. Đưa phần tử này về đúng vị trí và kết thúc thuật toán.
Ta phải thực thi tái cấu trúc heap, vun lại đống chính do sau khi lấy ra thành phần gốc heap, cấu trúc heap không còn nữa .
Lưu đồ thuật toán:
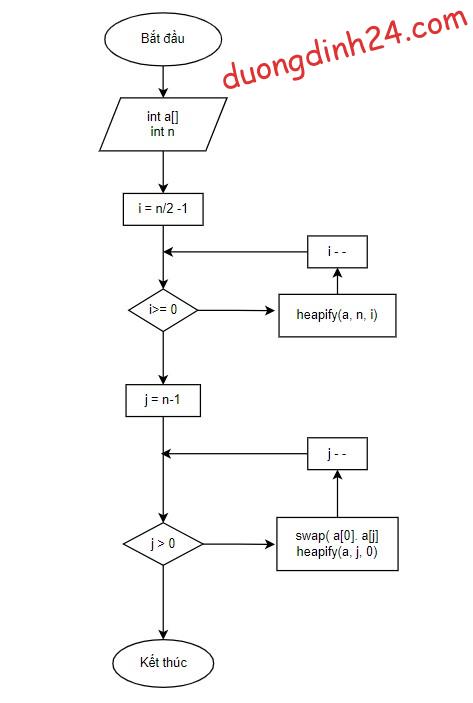 Lưu đồ thuật toán heap sort
Lưu đồ thuật toán heap sort
3. Cài đặt thuật toán heap sort C/C++
Phần này mình sẽ tiến hành heap sort bằng code C / C + +, để dễ tưởng tượng bạn nên xem thêm về cách hoạt động giải trí cụ thể animation của thuật toán tại đây .
Thuật toán được chia làm 2 phần :
- Hàm vun đống
- Hàm sắp xếp
3.1 Hàm vun đống một đỉnh
Hàm vun đống là hàm sẽ giúp tạo cấu trúc heap từ mảng bắt đầu. Ta sẽ viết hàm vun đống cho 1 đỉnh i, và một số ít nội dung mình cần chú ý quan tâm đó là .
- Nếu đỉnh cha có chỉ số là i thì con trái có chỉ số là: L = i * 2 + 1
Con phải có chỉ số là: r = i*2 +2
Trong đó L và r phải nhỏ hơn n (số phần tử của mảng) - Việc cần làm là tìm ra đỉnh lớn nhất trong 3 đỉnh: i, L, r
- Nếu đỉnh lớn nhất khác đỉnh ban đầu, ta tiến hành đổi chỗ. Đệ quy vun đống tại vị trí vừa đổi chỗ để vun các node tiếp theo.
Code C / C + + :
// Thuat toan sap xep vun dong
// Hàm vun đống cho một đỉnh
void heapify(int arr[], int n, int i){ // mảng arr, n - số phần tử, i - đỉnh cần vun đống
int max =i; // Lưu vị trí đỉnh max ban đầu
int l = i*2 +1; // Vị trí con trái
int r = l+1; // Vị trí con phải
if(l arr[max]){ // Nếu tồn tại con trái lớn hơn cha, gán max = L
max = l;
}
if(r arr[max]){ // Nếu tồn tại con phải lớn hơn arr[max], gán max = r
max = r;
}
if(max != i){ // Nếu max != i, tức là cha không phải lớn nhất
swap(arr[i], arr[max]); // Đổi chỗ cho phần tử lớn nhất làm cha
heapify(arr ,n, max); // Đệ quy vun các node phía dưới
}
}
3.2 Hàm sắp xếp vun đống
Hàm heapify bên trên giúp vun một đỉnh thành một đống, giờ đây ta chỉ cần vun hàng loạt dãy khởi đầu thành đống, sau đó lấy ra thành phần lớn nhất cho về cuối mảng. Lặp lại hành vi này cho tới khi thu được dãy sắp xếp .
- Để vun đống, ta sẽ phải vun từ dưới lên, tức là vun từ đỉnh cha cuối cùng của heap. Một mảng n phần tử sẽ có n/2 node cha.
- Đổi chỗ đỉnh gốc đống với phần tử cuối cùng của mảng. Như vậy phần tử lớn nhất sẽ nằm ở cuối mảng
- Giảm số lượng phần tử (loại bỏ phần tử cuối cùng đúng vị trí)
- Lặp lại việc vun đống và lấy phần tử cho tới khi còn 1 phần tử thì dừng
- Một mảng n phần tử sẽ phải thực hiện vun đống n lần
Code hàm Heap sort C / C + + :
// Ham sap xep vun dong
void heapSort(int arr[], int n){
// vun dong tu duoi len len de thanh heap
for(int i = n/2 - 1; i>=0; i--) // i chạy từ n/2 - 1 về 0 sẽ có n/2 đỉnh nhé!
heapify(arr,n, i); // Vun từng đỉnh
// Vòng lặp để thực hiện vun đống và lấy phần tử
for(int j = n-1 ; j>0; j--){ // chạy hết j == 1 sẽ dừng
// mỗi lần j - 1, tương đương với k xét phần tử cuối
swap(arr[0], arr[j] ); // đổi chỗ phần tử lớn nhất
heapify(arr, j, 0); // vun lại đống,
}
}
4. Đánh giá thuật toán
Sắp xếp vun đống là thuật toán sắp xếp có ứng dụng đến cấu trúc tài liệu heap, cây nhị phân. Chính cho nên vì thế đây là một thuật toán có độ phức tạp không quá cao nhưng lại khá phức tạp .
Bảng nhìn nhận thuật toán :
| Trường hợp | Độ phức tạp | Bộ nhớ sử dụng |
| Tốt nhất | O (n log n) | 1 |
| Trung bình | O (n log n) | 1 |
| Xấu nhất | O(n log n) | 1 |
Ưu điểm:
Xem thêm: Bài 2 – Cấu trúc thư mục Laravel – ITCOM
- Có độ phức tạp trung bình O (n log n) trong mọi trường hợp. Là một trong các thuật toán sắp xếp nhanh nhất
- Ít bị ảnh hưởng bởi dữ liệu đầu vào, có thể ứng dụng nhiều trong thực tế
Nhược điểm:
- Thuật toán cài đặt phức tạp, khó khăn trong việc hiểu thuật toán
- Là thuật toán sắp xếp không có tính ổn định
- Không tối ưu trong mọi trường hợp
Cảm ơn bạn đã chăm sóc bài viết, bài viết này mình có tìm hiểu thêm từ GeeksforGeeks. com và wikipedia. Rất mong nhận được góp ý từ phía bạn đọc để bài viết của mình triển khai xong hơn .
Source: https://final-blade.com
Category: Kiến thức Internet